
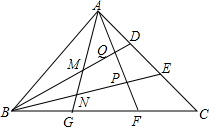
 △ABC面积为S,AD=DE=EC,BG=GF=FC,AG,AF与BD,BE分别交于M,N,P,Q,连接EF.
△ABC面积为S,AD=DE=EC,BG=GF=FC,AG,AF与BD,BE分别交于M,N,P,Q,连接EF.分析 (1)由AD=DE=EC,BG=GF=FC,可得出$\frac{CE}{AC}$=$\frac{CF}{CB}$,即可得出EF∥AB;
(2)设AG与BE交于N,AF与BE交于P,连接NC,ND,PC,PD,设△NGB的面积为x,△NDE的面积为y,则有△NCG的面积为2x,△NEA的面积为2y,得出△NGB的面积,设△PCF的面积为u,△PCE的面积为v,得出四边形PECF的面积是$\frac{1}{6}$S,可求出S四边形NGFP,设△ADQ的面积为c,△QBF的面积为d,可得△QBF的面积为$\frac{8}{21}$S,利用以正面积式子可得S四边形MNPQ=S△QBF-S△MGB-S四边形NGFP,即可求解.
解答 解:(1)如图,连接EF,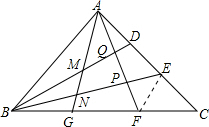
∵AD=DE=EC,BG=GF=FC,
∴$\frac{CE}{AC}$=$\frac{1}{3}$,$\frac{CF}{CB}$=$\frac{1}{3}$,
∴EF∥AB;
(2)如图1,设AG与BE交于N,AF与BE交于P,连接NC,ND,PC,PD,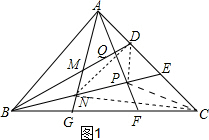
设△NGB的面积为x,△NDE的面积为y,则有△NCG的面积为2x,△NEA的面积为2y
∵△ABC的面积是S,且AD=DE=EC,BG=GF=FC,
∴△BCE,△ACF的面积是$\frac{1}{3}$S,△ACG的面积是$\frac{2}{3}$S
∴$\left\{\begin{array}{l}{3x+y=\frac{1}{3}S}\\{2x+3y=\frac{2}{3}S}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{1}{21}S}\\{y=\frac{4}{21}S}\end{array}\right.$
∴△NGB的面积是$\frac{1}{21}$S,
设△PCF的面积为u,△PCE的面积为v,则有$\left\{\begin{array}{l}{3u+v=\frac{1}{3}S}\\{u+3v=\frac{1}{3}S}\end{array}\right.$
∴4(uu+v)=$\frac{2}{3}$S,即uu+v=$\frac{1}{6}$S,即四边形PECF的面积是$\frac{1}{6}$S,
∴S四边形NGFP=$\frac{1}{3}$S-$\frac{1}{21}$S-$\frac{1}{6}$S=$\frac{5}{42}$S,
如图2,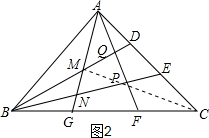
设△MGB的面积为a,△MAD的面积为b,
$\left\{\begin{array}{l}{3a+2b=\frac{2}{3}S}\\{2a+3b=\frac{2}{3}s}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{2}{15}S}\\{b=\frac{2}{15}s}\end{array}\right.$,
∴△MGB的面积为$\frac{2}{15}$S,
如图3,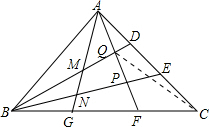
设△ADQ的面积为c,△QBF的面积为d,
$\left\{\begin{array}{l}{3c+\frac{1}{2}d=\frac{1}{3}S}\\{2c+\frac{3}{2}d=\frac{2}{3}S}\end{array}\right.$,解得$\left\{\begin{array}{l}{c=\frac{1}{21}S}\\{d=\frac{8}{21}S}\end{array}\right.$,
∴△QBF的面积为$\frac{8}{21}$S,
∴S四边形MNPQ=S△QBF-S△MGB-S四边形NGFP=$\frac{8}{21}$S-$\frac{2}{15}$S-$\frac{5}{42}$S=$\frac{9}{70}$S.
点评 此题主要考查了面积及等积变换,涉及平行线的判定,三角形的面积等知识,解题的关键是正确作出辅助线,利用三角形的面积列出方程组.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
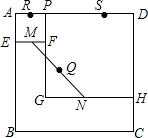 如图,四边形ABCD是边长为8的正方形,点R、S在边AD上,且AR=1,SD=2,点P是线段RS上的动点,分别以AP、PD为边在正方形ABCD内作正方形AEFP和PGHD,M、N分别为EF、GH的中点.连结MN,设MN的中点为0,则当点P从点R运动到点S时,点O移动的路径长为2.5.
如图,四边形ABCD是边长为8的正方形,点R、S在边AD上,且AR=1,SD=2,点P是线段RS上的动点,分别以AP、PD为边在正方形ABCD内作正方形AEFP和PGHD,M、N分别为EF、GH的中点.连结MN,设MN的中点为0,则当点P从点R运动到点S时,点O移动的路径长为2.5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com