
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
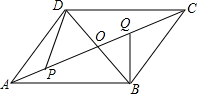 ?ABCD的对角线AC,BD交于点O,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP=OQ,连接BQ,DP.
?ABCD的对角线AC,BD交于点O,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP=OQ,连接BQ,DP.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这50名考生是总体的一个样本 | B. | 近1千名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 50名学生是样本容量 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
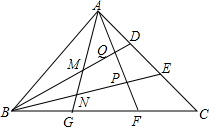 △ABC面积为S,AD=DE=EC,BG=GF=FC,AG,AF与BD,BE分别交于M,N,P,Q,连接EF.
△ABC面积为S,AD=DE=EC,BG=GF=FC,AG,AF与BD,BE分别交于M,N,P,Q,连接EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com