练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．计算：$\frac{1}{\sqrt{1}+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2000}+\sqrt{1999}}$．

    分析 先变形得到原式=$\frac{1}{\sqrt{2}+\sqrt{1}}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2000}+\sqrt{1999}}$，然后进行分母有理化后合并即可．

    解答 解：原式=$\frac{1}{\sqrt{2}+\sqrt{1}}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2000}+\sqrt{1999}}$
    =$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2000}$-$\sqrt{1999}$
    =$\sqrt{2000}$-1
    =20$\sqrt{5}$-1．

    点评 本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    5．计算（-1）2015+|-2|-（$\frac{1}{3}$）-1的值为-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算：
    （1）|-4$\frac{1}{3}$|•|-$\frac{3}{2}$|-|2|；
    （2）$\frac{|10-9|}{|1+9|}$-$\frac{|4-9|}{|4+9|}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．计算：-$\frac{3}{5}$+（-$\frac{2}{3}$）+（-$\frac{2}{5}$）+（+$\frac{1}{3}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．已知下列命题，其中真命题的个数是（　　）
    ①若a2=b2，则a=b；
    ②对角线互相垂直且相等的四边形是正方形；
    ③两组对角分别相等的四边形是平行四边形；
    ④在反比例函数y=$\frac{2}{x}$中，如果函数值y＜1时，那么自变量x＞2．
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．计算：-24-[1$\frac{4}{7}$+（-16）÷8]×（-$\frac{7}{2}$）3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：$\frac{bc-{a}^{2}}{ab}$+$\frac{ac-{b}^{2}}{bc}$+$\frac{ab-{c}^{2}}{ac}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：（$\frac{1}{4}$）0+（$\sqrt{3}$-1）（$\sqrt{3}$+1）+$\root{3}{-27}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

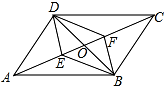    5．如图，在平行四边形ABCD中，对角线AC、BD相交于点O，E、F是对角线AC上的两点，给出下列四个条件：①AE=CF；②DE=BF；③∠ADE=∠CBF；④∠ABE=∠CDF．其中不能判定四边形DEBF是平行四边形的有（　　）
    A．0个B．1个C．2个D．3个

    查看答案和解析>>

    同步练习册答案