
【题目】将正整数1至2019按照一定规律排成下表:

记aij表示第i行第j个数,如a14=4表示第1行第4个数是4.
(1)直接写出a42=_________, a53=_________;
(2)①如果aij=2019,那么i=_________, j =_________;②用i,j表示aij=_____________;
(3) 将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和能否等于2027.若能,求出这5个数中的最小数,若不能说明理由。
【答案】26; 35; 253 3 aij=8(i-1) + j
(3)不能等于2027,理由见解析
【解析】
(1) 观察表格中的数据,根据数据的变化可求出a4, a53的值;
(2)①根据数据的变化,找出2019所在的位置;②由数的变化,找出aij的值;
(3)设这5个数中的最小数为x,则其余4个数可表示为x+4, x+9, x+11, x+18,由5个数之和为2027可得出关于x的一元-次方程,解之即可得出x的值,再找出x,(x+4) 所在的位置,由这两个数不在同一行可得出所覆盖的5个数之和不能等于2027.
解:(1)∵前面3行一共有![]() 个数,
个数,
∴第4行的第1个数为25,则第4行的第2个数为26,即![]() ;
;
∵前面4行一 共有![]() 个数,
个数,
∴第5行的第1个数为33,则第5行的第3个数为35,即![]() .
.
故答案为: 26; 35.
(2)①∵![]() ,
,
∴2019是第253行的第3个数,
∴i=253, j=3.
故答案为: 253; 3.
②根据题意得:![]() .
.
故答案为8 (i-1) +j.
(3)设这5个数中的最小数为x,则其余4个数可表示为x+4, x+9, x+11, x +18,
根据题意得:x+x+4+x+9+x+11 +x+ 18=2027,
解得x=397.
∵397=49×8+5,
∴397是第50行的第5个数,
而此时x+4=401是第51行的第1个数,与397不在同一行,
∴将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和不能等于2027.


科目:初中数学 来源: 题型:
【题目】公园内要铺设一段长方形步道,须用一些型号相同的灰色正方形地砖和一些型号相同 的白色等腰直角三角形地砖按如图所示方式排列.

(1) 若排列正方形地砖40块,则需使用三角形地砖____________块;
(2) 若排列三角形地砖2 020块,则需使用正方形地砖____________块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当m,n是正实数,且满足m+n=mn时,就称点P(m,![]() )为“完美点”,已知点A(0,5)与点M都在直线y=﹣x+b上,点B,C是“完美点”,且点B在线段AM上,若MC=
)为“完美点”,已知点A(0,5)与点M都在直线y=﹣x+b上,点B,C是“完美点”,且点B在线段AM上,若MC=![]() ,AM=4
,AM=4![]() ,求△MBC的面积
,求△MBC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年小张前五个月的奖金变化情况如下表(正数表示比前一月多的钱数,负数表示比前一月少的钱数,单位:元)
月份 | 一月 | 二月 | 三月 | 四月 | 五月 |
钱数变化 |
|
|
|
|
|
若2018年12月份小张的奖金为![]() 元.
元.
(1)用代数式表示2019年二月份小张的奖金为___________元;
(2)小张五月份所得奖金比二月份多多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
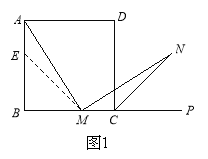
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
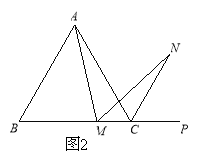
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
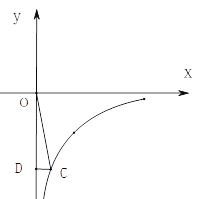
【题目】如图,点C在反比例函数y=![]() 的图象上,过点C作CD⊥y轴,交y轴负半轴于点D,且△ODC的面积是3.
的图象上,过点C作CD⊥y轴,交y轴负半轴于点D,且△ODC的面积是3.
(1)求反比例函数y=![]() 的解析式;
的解析式;
(2)若CD=1,求直线OC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
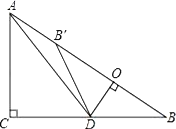
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如表所示
国外品牌 | 国内品牌 | |
进价(万元/部) | 0.44 | 0.2 |
售价(万元/部) | 0.5 | 0.25 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com