
 如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.
如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.分析 (1)DE与半圆O相切,理由为:连接OD,BD,由AB为半圆的直径,根据直径所对的圆周角为直角得到一个角为直角,可得出三角形BDC为直角三角形,又E为斜边BC的中点,利用中点的定义及斜边上的中线等于斜边的一半,得到ED=EB,利用等边对等角得到一对角相等,再由OD=OB,利用等边对等角得到一对角相等,根据∠EBO为直角,得到∠EBD与∠OBD和为90°,等量代换可得出∠ODE为直角,即DE与OD垂直,可得出DE为圆O的切线,得证;
(2)利用因式分解法求出x2-10x+24=0的解,再根据AB大于AD,且AD和AB为方程的解,确定出AB及AD的长,在直角三角形ABD中,利用勾股定理即可求出BD的长,然后根据三角形相似即可求得BC的长.
解答 (1)证明:DE与半圆O相切,理由为: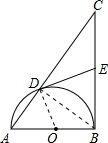
连接OD,BD,如图所示:
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△BDC中,E为BC的中点,
∴DE=BE=$\frac{1}{2}$BC,
∴∠EBD=∠EDB,
∵OB=OD,
∴∠OBD=∠ODB,
又∵∠ABC=90°,即∠OBD+∠EBD=90°,
∴∠EDB+∠ODB=90°,即∠ODE=90°,
∴DE为圆O的切线;
(2)解:方程x2-10x+24=0,
因式分解得:(x-4)(x-6)=0,
解得:x1=4,x2=6,
∵AD、AB的长是方程x2-10x+24=0的两个根,且AB>AD,
∴AD=4,AB=6,
∵AB是直径,
∴∠ADB=90°,
在Rt△ABD中,根据勾股定理得:BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=2$\sqrt{5}$,
∵△ABD∽△ACB,
∴$\frac{BC}{BD}$=$\frac{AB}{AD}$,即$\frac{BC}{2\sqrt{5}}$=$\frac{6}{4}$,
∴BC=3$\sqrt{5}$.
点评 此题考查了切线的判定,勾股定理,直角三角形斜边上中线的性质,圆周角定理,以及利用分解因式的方法解一元二次方程,熟练掌握定理及性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
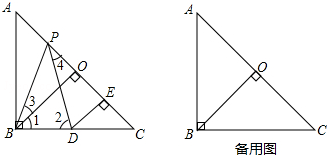
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 苍溪嘉陵江三桥是连接苍溪老城与江南老区的一座下承式钢管混凝土柔性系杆拱桥,它的桥拱是抛物线形状,两桥墩的距离是240米,桥拱的拱高60米.
苍溪嘉陵江三桥是连接苍溪老城与江南老区的一座下承式钢管混凝土柔性系杆拱桥,它的桥拱是抛物线形状,两桥墩的距离是240米,桥拱的拱高60米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
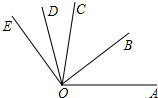 如图,OB是∠A0C的平分线,OD是∠COE的平分线.
如图,OB是∠A0C的平分线,OD是∠COE的平分线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com