
 苍溪嘉陵江三桥是连接苍溪老城与江南老区的一座下承式钢管混凝土柔性系杆拱桥,它的桥拱是抛物线形状,两桥墩的距离是240米,桥拱的拱高60米.
苍溪嘉陵江三桥是连接苍溪老城与江南老区的一座下承式钢管混凝土柔性系杆拱桥,它的桥拱是抛物线形状,两桥墩的距离是240米,桥拱的拱高60米.分析 (1)根据题目中的信息,可以设出抛物线的解析式,然后根据题目中的信息即可求得该抛物线的解析式;
(2)将x=60代入第一问求得的抛物线的解析式即可解答本题.
解答 解:(1)设此桥拱的抛物线解析式为:y=a(x-120)2+60
∵点(0,0)在此函数所在的图象上,
∴0=a×(0-120)2+60,
解得a=$-\frac{1}{240}$.
即此桥拱的抛物线的解析式是:y=$-\frac{1}{240}(x-120)^{2}+60$;
(2)将x=60代入y=$-\frac{1}{240}(x-120)^{2}+60$,得
y=45.
即吊杆在桥面上的拉点A距桥墩60米处,则此吊杆的长度是45米.
点评 本题考查二次函数的应用,解题的关键是将该抛物线与二次函数结合在一起,选择合适的平面直角坐标系,设出顶点式,求出抛物线的解析式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1440}{x}=\frac{1440}{x+100}+10$ | B. | $\frac{1440}{x-100}-\frac{1440}{x}=10$ | ||
| C. | $\frac{1440}{x}=\frac{1440}{x-100}+10$ | D. | $\frac{1440}{x+100}-\frac{1440}{x}=10$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
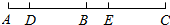 如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE=$\frac{1}{5}$AE,若DB=12.
如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE=$\frac{1}{5}$AE,若DB=12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.
如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com