
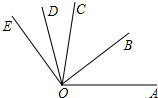
 如图,OB是∠A0C的平分线,OD是∠COE的平分线.
如图,OB是∠A0C的平分线,OD是∠COE的平分线.分析 (1)求得∠AOC=80°,然后求得∠COD=30°,∠BOC=∠AOC=40°,根据∠BOD=∠BOC+∠COD即可求出∠MON的度数.
(2)结合图形,根据角的和差,以及角平分线的定义,找到∠BOD与∠AOE的关系,即可求出∠DOC+∠BOC=90°;
(3)结合图形,根据角的和差,以及角平分线的定义,找到∠BOD与∠AOE的关系,即可求出∠BOD的度数.
解答 解:(1)∵OB是∠A0C的平分线,OD是∠COE的平分线,∠AOE=140°,∠EOD=30°,
∴∠EOC=2∠EOD=2×30°=60°,∠COD=∠EOD=30°,
∴∠AOC=∠AOE-∠EOC=140°-60°=80°,
∴∠BOC=$\frac{1}{2}$∠AOC=40°,
∴∠BOD=∠BOC+∠COD=70°;
(2)∠DOC+∠BOC=90°,
理由:∵∠DOC=$\frac{1}{2}$∠EOC,∠BOC=$\frac{1}{2}$∠AOC,
∴∠DOC+∠BOC=$\frac{1}{2}$(∠EOC+∠AOC)=$\frac{1}{2}$∠AOE,
∵∠AOE=180°,
∴∠DOC+∠BOC=$\frac{1}{2}$×180°=90°;
(3)∵∠DOC=$\frac{1}{2}$∠EOC,∠BOC=$\frac{1}{2}$∠AOC,
∴∠DOC+∠BOC=$\frac{1}{2}$(∠EOC+∠AOC)=$\frac{1}{2}$∠AOE,
∵∠AOE=α,
∴∠DOC+∠BOC=$\frac{α}{2}$;
故答案为70°;$\frac{α}{2}$.
点评 本题考查了角平分线定义和角的计算,关键是求出∠BOC、∠COD的度数和得出∠BOD=∠BOC+∠COD.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
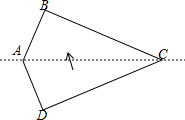 如图,在四边形纸片ABCD中,AB=AD,CB=CD,∠B=∠D=90°,∠A=135°.将纸片先沿直线AC对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为$2\sqrt{2}$的平行四边形,则CD=2+$\sqrt{2}$或2+2$\sqrt{2}$.
如图,在四边形纸片ABCD中,AB=AD,CB=CD,∠B=∠D=90°,∠A=135°.将纸片先沿直线AC对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为$2\sqrt{2}$的平行四边形,则CD=2+$\sqrt{2}$或2+2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.
如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 南京市与连云港市两地相距300km,甲车在南京市,乙车在连云港市,两车同时出发,相向而行,在A地相遇.为节约费用(两车相遇并换货后,均需按原路返回出发地).两车换货后,甲车立即按原路返回南京市,而乙车又停留1小时后按原路返回连云港市.设每车在行驶过程中速度保持不变,两车间的距离y(km)与时间x(h)的函数关系如图所示,根据所提供的信息,回答下列问题:
南京市与连云港市两地相距300km,甲车在南京市,乙车在连云港市,两车同时出发,相向而行,在A地相遇.为节约费用(两车相遇并换货后,均需按原路返回出发地).两车换货后,甲车立即按原路返回南京市,而乙车又停留1小时后按原路返回连云港市.设每车在行驶过程中速度保持不变,两车间的距离y(km)与时间x(h)的函数关系如图所示,根据所提供的信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com