
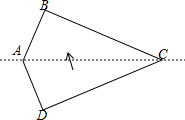
 如图,在四边形纸片ABCD中,AB=AD,CB=CD,∠B=∠D=90°,∠A=135°.将纸片先沿直线AC对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为$2\sqrt{2}$的平行四边形,则CD=2+$\sqrt{2}$或2+2$\sqrt{2}$.
如图,在四边形纸片ABCD中,AB=AD,CB=CD,∠B=∠D=90°,∠A=135°.将纸片先沿直线AC对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为$2\sqrt{2}$的平行四边形,则CD=2+$\sqrt{2}$或2+2$\sqrt{2}$. 分析 根据题意结合裁剪的方法得出符合题意的图形有两个,分别利用菱形的判定与性质以及勾股定理得出CD的长.
解答 解:如图1所示:
延长BE交CD于点N,过点A作AT⊥BE于点T,
当四边形ABED为平行四边形,
∵AB=AD,
∴四边形ABED是菱形,
∵∠ABC=∠ADC=90°,∠BAD=135°,AD∥BN,AB∥DE,
∴∠ABT=45°,∠BAT=45°,∠ABT=∠DEN=45°,∠END=90°,
则∠NDE=45°,
∵四边形ABCE面积为2$\sqrt{2}$,
∴设AT=x,则AB=BE=ED=$\sqrt{2}$x,
故$\sqrt{2}$x×x=2$\sqrt{2}$,
解得:x=$\sqrt{2}$(负数舍去),
则BE=ED=2,EN=$\sqrt{2}$,
故DC=DN+NC=$\sqrt{2}$+$\sqrt{2}$+2=2+2$\sqrt{2}$;
如图2,
当四边形AECF是平行四边形,
∵AE=AF,
∴平行四边形AECF是菱形,
∵∠B=∠D=90°,∠BAD=135°,
∴∠BCA=∠DCA=22.5°,
∵AE=CE,
∴∠AEB=45°,
∴设AB=y,则BE=y,AE=$\sqrt{2}$y,
∵四边形AECF面积为2$\sqrt{2}$,
∴AB×CE=$\sqrt{2}$y2=2$\sqrt{2}$,
解得:y=$\sqrt{2}$,故CE=2,BE=$\sqrt{2}$,
则CD=BC=2+$\sqrt{2}$,
综上所述:CD的值为:2+$\sqrt{2}$或2+2$\sqrt{2}$.
故答案为:$2+2\sqrt{2}$或$2+\sqrt{2}$.
点评 此题主要考查了翻折变换,剪纸问题以及勾股定理和平行四边形的性质,根据题意画出正确图形是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
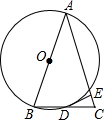 如图,△ABC的边AB为⊙O的直径,BC与⊙O交于点D,D为BC的中点,过点D作DE⊥AC于E.
如图,△ABC的边AB为⊙O的直径,BC与⊙O交于点D,D为BC的中点,过点D作DE⊥AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
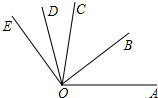 如图,OB是∠A0C的平分线,OD是∠COE的平分线.
如图,OB是∠A0C的平分线,OD是∠COE的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 身高为1.8m 的运动员小王进行投篮训练,已知篮圈中心与地面的垂直距离为3.05 m,小王站在与篮圈中心的水平距离4m的地方进行跳投,球的运动路线一条抛物线,当球运行的水平距离为2.5m时,球达到距离地面3.5m的最高点,运行一段时间后篮球最后恰好落入篮圈.
身高为1.8m 的运动员小王进行投篮训练,已知篮圈中心与地面的垂直距离为3.05 m,小王站在与篮圈中心的水平距离4m的地方进行跳投,球的运动路线一条抛物线,当球运行的水平距离为2.5m时,球达到距离地面3.5m的最高点,运行一段时间后篮球最后恰好落入篮圈.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 3 | 4 | 5 |
| ax2+bx+c | 0.5 | -0.5 | -1 |
| A. | x<3 | B. | x<2 | C. | 4<x<5 | D. | 3<x<4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com