
分析 先把括号内通分和除法运算化为乘法运算,再把分子分母因式分解后约分得到原式=$\frac{ab}{a-b}$,然后把a、b的值代入计算即可.
解答 解:原式=$\frac{(a+b)(a-b)}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{(a+b)(a-b)}{a}$•$\frac{a}{(a-b)^{2}}$
=$\frac{a+b}{a-b}$,
当a=3,b=2时,原式=$\frac{3+2}{3-2}$=5.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案科目:初中数学 来源: 题型:解答题
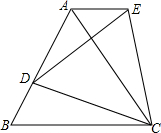 如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.
如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,AC与BD相交于点O,E为AD上的一点,连接BE,点G在BE上,连结OG并延长交AD于点F,若∠FGE=45°.
如图,在正方形ABCD中,AC与BD相交于点O,E为AD上的一点,连接BE,点G在BE上,连结OG并延长交AD于点F,若∠FGE=45°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:
沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
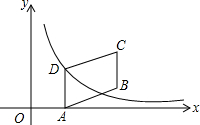 如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.
如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com