
【题目】(1)阅读理解
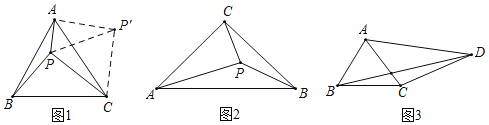
利用旋转变换解决数学问题是一种常用的方法.如图1,点P是等边三角形ABC内一点,PA=1,PB=![]() ,PC=2.求∠BPC的度数.
,PC=2.求∠BPC的度数.
为利用已知条件,不妨把△BPC绕点C顺时针旋转60°得△AP′C,连接PP′,则PP′的长为_____;在△PAP′中,易证∠PAP′=90°,且∠PP′A的度数为_____,综上可得∠BPC的度数为_____;
(2)类比迁移
如图2,点P是等腰Rt△ABC内的一点,∠ACB=90°,PA=2,PB=![]() ,PC=1,求∠APC的度数;
,PC=1,求∠APC的度数;
(3)拓展应用
如图3,在四边形ABCD中,BC=3,CD=5,AB=AC=![]() AD.∠BAC=2∠ADC,请直接写出BD的长.
AD.∠BAC=2∠ADC,请直接写出BD的长.
【答案】(1)2;30°;90°;(2)∠APC=90°;(3)BD=![]() .
.
【解析】
(1)由旋转性质、等边三角形的判定可知△CP′P是等边三角形,由等边三角形的性质知∠CP′P=60°,根据勾股定理逆定理可得△AP′P是直角三角形,继而可得答案.
(2)如图2,把△BPC绕点C顺时针旋转90°得△AP'C,连接PP′,同理可得△CP′P是等腰直角三角形和△AP′P是直角三角形,所以∠APC=90°;
(3)如图3,将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,根据勾股定理求CG的长,就可以得BD的长.
解:(1)把△BPC绕点C顺时针旋转60°得△AP'C,连接PP′(如图1).

由旋转的性质知△CP′P是等边三角形;
∴P′A=PB=![]() 、∠CP′P=60°、P′P=PC=2,
、∠CP′P=60°、P′P=PC=2,
在△AP′P中,∵AP2+P′A2=12+(![]() )2=4=PP′2;
)2=4=PP′2;
∴△AP′P是直角三角形;
∴∠P′AP=90°.
∵PA=![]() PC,
PC,
∴∠AP′P=30°;
∴∠BPC=∠CP′A=∠CP′P+∠AP′P=60°+30°=90°.
故答案为:2;30°;90°;
(2)如图2,把△BPC绕点C顺时针旋转90°得△AP'C,连接PP′.
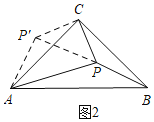
由旋转的性质知△CP′P是等腰直角三角形;
∴P′C=PC=1,∠CPP′=45°、P′P=![]() ,PB=AP'=
,PB=AP'=![]() ,
,
在△AP′P中,∵AP'2+P′P2=(![]() )2+(
)2+(![]() )2=2=AP2;
)2=2=AP2;
∴△AP′P是直角三角形;
∴∠AP′P=90°.
∴∠APP'=45°
∴∠APC=∠APP'+∠CPP'=45°+45°=90°
(3)如图3,
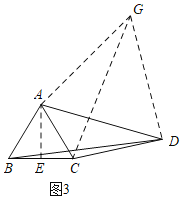
∵AB=AC,
将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,
∵∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴△ABC∽△ADG,
∵AD=2AB,
∴DG=2BC=6,
过A作AE⊥BC于E,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADG+∠ADC=90°,
∴∠GDC=90°,
∴CG=![]() ,
,
∴BD=CG=![]() .
.


科目:初中数学 来源: 题型:
【题目】某企业生产一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量![]() (套)与每套的售价
(套)与每套的售价![]() (万元)之间满足关系式
(万元)之间满足关系式![]() ,月产量
,月产量![]() (套)与生产总成本
(套)与生产总成本![]() (万元)存在如图所示的函数关系.
(万元)存在如图所示的函数关系.
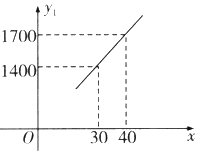
(1)直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求月产量![]() 的取值范围;
的取值范围;
(3)当月产量![]() (套)为多少时,这种产品的利润
(套)为多少时,这种产品的利润![]() (万元)最大?最大利润是多少?
(万元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
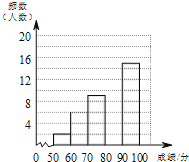
【题目】为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
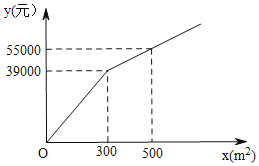
【题目】为了美化环境,建设宜居衡阳,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)求y与x的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共1000m2,若甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的3倍,那么应该怎忙分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
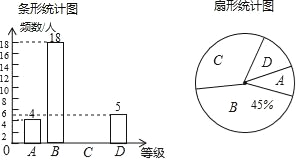
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】父亲节即将到来之际,某商店准备购进![]() 、
、![]() 两种男装进行销售,其中每套
两种男装进行销售,其中每套![]() 种男装的进价比每套
种男装的进价比每套![]() 种男装的进价多
种男装的进价多![]() 元用
元用![]() 元购进
元购进![]() 种男装的数量是用
种男装的数量是用![]() 元购进
元购进![]() 种男装数量的
种男装数量的![]() 倍.
倍.
(1)求每套![]() 种男装和每套
种男装和每套![]() 种男装的进价各是多少元:
种男装的进价各是多少元:
(2)若该商店本次购进![]() 种男装的数量比购进
种男装的数量比购进![]() 种男装的数量的
种男装的数量的![]() 倍还多
倍还多![]() 套,该商店每套
套,该商店每套![]() 种男装的销售价格为
种男装的销售价格为![]() 元,每套
元,每套![]() 种男装的销售价格为
种男装的销售价格为![]() 元,若将本次购进的
元,若将本次购进的![]() 、
、![]() 两种男装全部售出后获得的利润不少于
两种男装全部售出后获得的利润不少于![]() 元,那么该商店至少需要购进
元,那么该商店至少需要购进![]() 种男装多少套?
种男装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明想测量河对岸的一幢高楼AB的高度,小明在河边C处测得楼顶A的仰角是60°距C处60米的E处有幢楼房,小明从该楼房中距地面20米的D处测得楼顶A的仰角是30°(点B.C.E在同一直线上且AB、DE均与地面BE处置),求楼AB的高________.![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
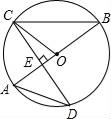
【题目】如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E.
(1)若∠A=48°,求∠OCE的度数;
(2)若CD=4![]() ,AE=2,求圆O的半径.
,AE=2,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com