
【题目】某企业生产一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量![]() (套)与每套的售价
(套)与每套的售价![]() (万元)之间满足关系式
(万元)之间满足关系式![]() ,月产量
,月产量![]() (套)与生产总成本
(套)与生产总成本![]() (万元)存在如图所示的函数关系.
(万元)存在如图所示的函数关系.
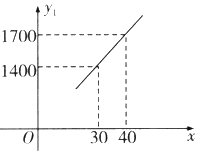
(1)直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求月产量![]() 的取值范围;
的取值范围;
(3)当月产量![]() (套)为多少时,这种产品的利润
(套)为多少时,这种产品的利润![]() (万元)最大?最大利润是多少?
(万元)最大?最大利润是多少?
【答案】(1)![]() (2)25≤x≤35 (3)当月产量为35套时,这种产品的利润最大,最大利润是2650万元
(2)25≤x≤35 (3)当月产量为35套时,这种产品的利润最大,最大利润是2650万元
【解析】
(1)、利用待定系数法求出y与x之间的函数关系式;(2)、根据生产成本不高于50万元,每套产品的售价不低于120万元列出不等式组,从而求出x的取值范围;(3)、根据题意列出w与x的函数关系式,然后根据函数的增减性以及x的取值范围得出最大值.
(1)![]()
(2)由题意得:![]() ,
,
解得:25≤x≤35 即月产量x的范围是25≤x≤35
(3)、由题意得: ![]()
![]()
![]()
∵![]() ∴当25≤x≤35时,w随x的增大而增大,
∴当25≤x≤35时,w随x的增大而增大,
∴当 ![]() 时,W有最大值,最大值是2650,
时,W有最大值,最大值是2650,
即当月产量为35套时,这种产品的利润最大,最大利润是2650万元.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是半径为2的⊙O的直径,直线l与AB所在直线垂直,垂足为C,OC=3,P是圆上异于A、B的动点,直线AP、BP分别交l于M、N两点.
(1)当∠A=30°时,MN的长是 ;
(2)求证:MCCN是定值;
(3)MN是否存在最大或最小值,若存在,请写出相应的最值,若不存在,请说明理由;
(4)以MN为直径的一系列圆是否经过一个定点,若是,请确定该定点的位置,若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国为了实现到2020年达到全面小康社会的目标,近几年加大了扶贫工作的力度,合肥市某知名企业为了帮助某小型企业脱贫,投产一种书包,每个书包制造成本为18元,试销过程中发现,每月销售量y(万个)与销售单价x(元)之间的关系可以近似看作一次函数y=kx+b,据统计当售价定为30元/个时,每月销售40万个,当售价定为35元/个时,每月销售30万个.
(1)请求出k、b的值.
(2)写出每月的利润w(万元)与销售单价x(元)之间的函数解析式.
(3)该小型企业在经营中,每月销售单价始终保持在25≤x≤36元之间,求该小型企业每月获得利润w(万元)的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣x+1的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市的重大惠民工程--公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积![]() 单位:百万平方米
单位:百万平方米![]() ,与时间x的关系是
,与时间x的关系是![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() ;后4年,每年竣工投入使用的公租房面积
;后4年,每年竣工投入使用的公租房面积![]() 单位:百万平方米
单位:百万平方米![]() ,与时间x的关系是
,与时间x的关系是![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() 假设每年的公租房全部出租完
假设每年的公租房全部出租完![]() 另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金
另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金![]() 单位:元
单位:元![]() 与时间
与时间![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() 满足一次函数关系如下表:
满足一次函数关系如下表:
| 50 | 52 | 54 | 56 | 58 |
|
| 1 | 2 | 3 | 4 | 5 |
|
![]() 求出z与x的函数关系式;
求出z与x的函数关系式;
![]() 求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
![]() 若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高
若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高![]() ,这样可解决住房的人数将比第6年减少
,这样可解决住房的人数将比第6年减少![]() ,求a的值.
,求a的值.
![]() 参考数据:
参考数据: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象过点A(3,0),对称轴为直线x=1,给出以下结论:①abc<0;②3a+c=0;③ax2+bx≤a+b;④若M(﹣0.5,y1)、N(2.5,y2)为函数图象上的两点,则y1<y2.其中正确的是( )
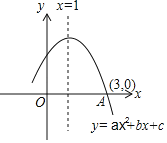
A.①③④B.①②3④C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )

A.红红不是胜就是输,所以红红胜的概率为![]()
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为![]()
D.娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
科目:初中数学 来源: 题型:
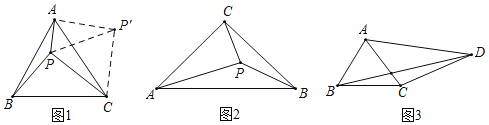
【题目】(1)阅读理解
利用旋转变换解决数学问题是一种常用的方法.如图1,点P是等边三角形ABC内一点,PA=1,PB=![]() ,PC=2.求∠BPC的度数.
,PC=2.求∠BPC的度数.
为利用已知条件,不妨把△BPC绕点C顺时针旋转60°得△AP′C,连接PP′,则PP′的长为_____;在△PAP′中,易证∠PAP′=90°,且∠PP′A的度数为_____,综上可得∠BPC的度数为_____;
(2)类比迁移
如图2,点P是等腰Rt△ABC内的一点,∠ACB=90°,PA=2,PB=![]() ,PC=1,求∠APC的度数;
,PC=1,求∠APC的度数;
(3)拓展应用
如图3,在四边形ABCD中,BC=3,CD=5,AB=AC=![]() AD.∠BAC=2∠ADC,请直接写出BD的长.
AD.∠BAC=2∠ADC,请直接写出BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com