
【题目】如图,AB是半径为2的⊙O的直径,直线l与AB所在直线垂直,垂足为C,OC=3,P是圆上异于A、B的动点,直线AP、BP分别交l于M、N两点.
(1)当∠A=30°时,MN的长是 ;
(2)求证:MCCN是定值;
(3)MN是否存在最大或最小值,若存在,请写出相应的最值,若不存在,请说明理由;
(4)以MN为直径的一系列圆是否经过一个定点,若是,请确定该定点的位置,若不是,请说明理由.

【答案】(1)![]() ;(2)MCNC=5;(3)a+b的最小值为2
;(2)MCNC=5;(3)a+b的最小值为2![]() ;(4)以MN为直径的一系列圆经过定点D,此定点D在直线AB上且CD的长为
;(4)以MN为直径的一系列圆经过定点D,此定点D在直线AB上且CD的长为![]() .
.
【解析】
(1)由题意得AO=OB=2、OC=3、AC=5、BC=1,根据MC=ACtan∠A=![]()
![]() 、CN=
、CN=![]() 可得答案;
可得答案;
(2)证△ACM∽△NCB得![]() ,由此即可求得答案;
,由此即可求得答案;
(3)设MC=a、NC=b,由(2)知ab=5,由P是圆上异于A、B的动点知a>0,可得b=![]() (a>0),根据反比例函数的性质得a+b不存在最大值,当a=b时,a+b最小,据此求解可得;
(a>0),根据反比例函数的性质得a+b不存在最大值,当a=b时,a+b最小,据此求解可得;
(4)设该圆与AC的交点为D,连接DM、DN,证△MDC∽△DNC得![]() ,即MCNC=DC2=5,即DC=
,即MCNC=DC2=5,即DC=![]() ,据此知以MN为直径的一系列圆经过定点D,此顶点D在直线AB上且CD的长为
,据此知以MN为直径的一系列圆经过定点D,此顶点D在直线AB上且CD的长为![]() .
.
(1)如图所示,根据题意知,AO=OB=2、OC=3,

则AC=OA+OC=5,BC=OC﹣OB=1,
∵AC⊥直线l,
∴∠ACM=∠ACN=90°,
∴MC=ACtan∠A=5×![]() =
=![]() ,
,
∵∠ABP=∠NBC,
∴∠BNC=∠A=30°,
∴CN= ,
,
则MN=MC+CN=![]() +
+![]() =
=![]() ,
,
故答案为:![]() ;
;
(2)∵∠ACM=∠NCB=90°,∠A=∠BNC,
∴△ACM∽△NCB,
∴![]() ,
,
即MCNC=ACBC=5×1=5;
(3)设MC=a、NC=b,
由(2)知ab=5,
∵P是圆上异于A、B的动点,
∴a>0,
∴b=![]() (a>0),
(a>0),
根据反比例函数的性质知,a+b不存在最大值,当a=b时,a+b最小,
由a=b得a=![]() ,解之得a=
,解之得a=![]() (负值舍去),此时b=
(负值舍去),此时b=![]() ,
,
此时a+b的最小值为2![]() ;
;
(4)如图,设该圆与AC的交点为D,连接DM、DN,
∵MN为直径,
∴∠MDN=90°,
则∠MDC+∠NDC=90°,
∵∠DCM=∠DCN=90°,
∴∠MDC+∠DMC=90°,
∴∠NDC=∠DMC,
则△MDC∽△DNC,
∴![]() ,即MCNC=DC2,
,即MCNC=DC2,
由(2)知MCNC=5,
∴DC2=5,
∴DC=![]() ,
,
∴以MN为直径的一系列圆经过定点D,此定点D在直线AB上且CD的长为![]() .
.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图:图象①②③均是以P0为圆心,1个单位长度为半径的扇形,将图形①②③分别沿东北,正南,西北方向同时平移,每次移动一个单位长度,第一次移动后图形①②③的圆心依次为P1P2P3,第二次移动后图形①②③的圆心依次为P4P5P6…,依此规律,P0P2018=_____个单位长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲骑电瓶车,乙骑自行车从湖州西山漾公园丝绸小镇门口出发沿同一路线匀速前往太湖龙之梦乐园.设乙行驶的时间为x(h),甲、乙两人距出发点的路程S甲、S乙关于x的函数图像如图①所示;甲、乙两人之间的路程差y关于x的函数图像如图②所示:
请你解决以下问题
(1)甲的速度是_____km/h;乙的速度是______km/h;
(2)对比图①、②可知:a=______;b=_____.
(3)乙出发多少时间,甲、乙两人路程差为7.5km?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.
求证:(1)△ABE≌△CDF;
(2)四边形BFDE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.
),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量![]() (套)与每套的售价
(套)与每套的售价![]() (万元)之间满足关系式
(万元)之间满足关系式![]() ,月产量
,月产量![]() (套)与生产总成本
(套)与生产总成本![]() (万元)存在如图所示的函数关系.
(万元)存在如图所示的函数关系.
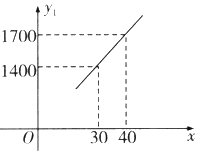
(1)直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求月产量![]() 的取值范围;
的取值范围;
(3)当月产量![]() (套)为多少时,这种产品的利润
(套)为多少时,这种产品的利润![]() (万元)最大?最大利润是多少?
(万元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
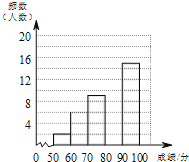
【题目】为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com