
【题目】我国为了实现到2020年达到全面小康社会的目标,近几年加大了扶贫工作的力度,合肥市某知名企业为了帮助某小型企业脱贫,投产一种书包,每个书包制造成本为18元,试销过程中发现,每月销售量y(万个)与销售单价x(元)之间的关系可以近似看作一次函数y=kx+b,据统计当售价定为30元/个时,每月销售40万个,当售价定为35元/个时,每月销售30万个.
(1)请求出k、b的值.
(2)写出每月的利润w(万元)与销售单价x(元)之间的函数解析式.
(3)该小型企业在经营中,每月销售单价始终保持在25≤x≤36元之间,求该小型企业每月获得利润w(万元)的范围.
【答案】(1)k的值为﹣2,b的值为100;(2)w=﹣2x2+136x﹣1800;(3)该小型企业每月获得利润w(万元)的范围是350≤w≤512.
【解析】
(1)待定系数法求出k和b的值即可;
(2)利用(售价-成本)乘以销售量等于利润可列式求解;
(3)根据二次函数的顶点值,及顶点左右两侧增减变化的性质来求解即可.
解:(1)由题意得:![]() ,
,
解得![]() .
.
答:k的值为﹣2,b的值为100;
(2)由题意得w=(x﹣18)(﹣2x+100)=﹣2x2+136x﹣1800,
答:函数解析式为:w=﹣2x2+136x﹣1800;
(3)∵w=﹣2x2+136x﹣1800=﹣2(x﹣34)2+512,
∴当x=34时,w取最大值,最大值为512;
当x<34时,w随着x的增大而增大;
当x>34时,w随着x的增大而减小.
∵当x=25时,
w=﹣2×252+136×25﹣1800=350;
当x=36时,
w=﹣2×362+136×36﹣1800=504.
综上,w的范围为350≤w≤512.
答:该小型企业每月获得利润w(万元)的范围是350≤w≤512.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x、y轴的正半轴上,顶点B的坐标为(4,2)点M是边BC上的一个动点(不与B、C重合),反比例函数![]() (k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
(k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.

(1)当点M是边BC的中点时,求反比例函数的表达式;
(2)在点M的运动过程中,试证明:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲骑电瓶车,乙骑自行车从湖州西山漾公园丝绸小镇门口出发沿同一路线匀速前往太湖龙之梦乐园.设乙行驶的时间为x(h),甲、乙两人距出发点的路程S甲、S乙关于x的函数图像如图①所示;甲、乙两人之间的路程差y关于x的函数图像如图②所示:
请你解决以下问题
(1)甲的速度是_____km/h;乙的速度是______km/h;
(2)对比图①、②可知:a=______;b=_____.
(3)乙出发多少时间,甲、乙两人路程差为7.5km?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.
),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法:①当n很大时,估计指针落在“铅笔”区域的频率大约是0.70;②假如你去转动转盘一次,获得铅笔的概率大约是0.70;③如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次;④转动转盘10次,一定有3次获得文具盒.中正确的是_____
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量![]() (套)与每套的售价
(套)与每套的售价![]() (万元)之间满足关系式
(万元)之间满足关系式![]() ,月产量
,月产量![]() (套)与生产总成本
(套)与生产总成本![]() (万元)存在如图所示的函数关系.
(万元)存在如图所示的函数关系.
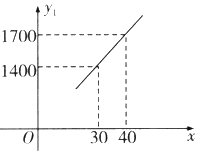
(1)直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求月产量![]() 的取值范围;
的取值范围;
(3)当月产量![]() (套)为多少时,这种产品的利润
(套)为多少时,这种产品的利润![]() (万元)最大?最大利润是多少?
(万元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
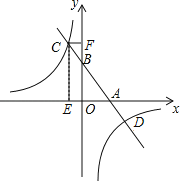
【题目】如图,已知一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=![]() 交于点C,D.作CE⊥x轴,垂足为E,CF⊥y轴,垂足为F.点B为OF的中点,四边形OECF的面积为16,点D的坐标为(4,﹣b).
交于点C,D.作CE⊥x轴,垂足为E,CF⊥y轴,垂足为F.点B为OF的中点,四边形OECF的面积为16,点D的坐标为(4,﹣b).
(1)求一次函数表达式和反比例函数表达式;
(2)求出点C坐标,并根据图象直接写出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
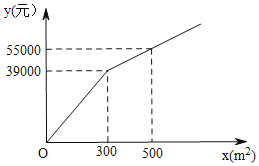
【题目】为了美化环境,建设宜居衡阳,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)求y与x的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共1000m2,若甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的3倍,那么应该怎忙分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com