
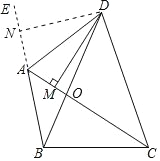
【题目】 如图,在△DBC 中,DB=DC,A 为△DBC 外一点,且∠BAC=∠BDC,DM⊥AC 于 M.
(1)求证:AD 平分△ABC 的外角;
(2)判断 AM、AC、AB 有怎样的数量关系,并证明你的结论.

【答案】(1)见解析;(2)AC﹣AB=2AM.
【解析】
1)如图 1 中,作 DN⊥BA 交 BA 的延长线于点 N.只要证明△DNB≌
△DMC(AAS),即可推出 DN=DM 解决问题;
(2)结论:AC﹣AB=2AM.利用全等三角形的性质即可证明;
(1)证明:如图 1 中,作 DN⊥BA 交 BA 的延长线于点 N.
∵∠BAO=∠ODC,∠AOB=∠DOC,
∴∠ABO=∠DCO,
∵DM⊥AC,DN⊥AB,
∴∠DNB=∠DMC=90°,
∵DB=DC,
∴△DNB≌△DMC(AAS),
∴DN=DM,∵DM⊥AC,DN⊥AB,
AD 平分△ABC 的外角;
(2)结论:AC﹣AB=2AM.
理由:∵DN=DM,DA=DA,∠DNA=∠DMA=90°,
∴Rt△DNA≌Rt△DMA(HL),
∴AN=AM,
∵△DNB≌△DMC(AAS),
∴BN=CM,
∴AC﹣AB=AM+CN﹣(BN﹣AN)=2AM.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
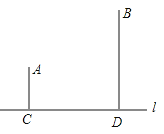
【题目】如图,牧童在A处放牛,其家在B处,A、B到河岸l的距离分别为AC=1km,BD=3km,且CD=3km.
(1)牧童从A处将牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?请用尺规在图中画出饮水的位置(保留作图痕迹,不写作法),并说明理由.
(2)求出(1)中的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位数,若十位上的数字是百位数字与个位数字的和,我们称这个三位数叫“圣诞数”,并且把这个“圣诞数”的前两位组成的两位数记为m,后两位组成的两位数记为n,并规定d=![]() 。如一个三位数385,
。如一个三位数385,![]() 3+5=8,
3+5=8,![]() 385是“圣诞数”,且m=38,n=85,则d=
385是“圣诞数”,且m=38,n=85,则d=![]() =
=![]() .
.
(1)写出最小的“圣诞数”;
(2)求证:任意一个“圣诞数”是11的倍数;
(3)求出所有能被8整除的“圣诞数”,并直接写出这些“圣诞数”中d的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形 ABCD 的面积为 16,△ABE 是等边三角形,点 E 在正方形 ABCD 内,在对角线 AC 上有一点 P,使 PD+PE 的和最小,则这个最小值为_____________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
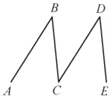
【题目】如图,如果AB∥CD,∠B=37°,∠D=37°,那么BC与DE平行吗?完成下面解答过中的填空或填写理由.
解:∵AB∥CD ( 已知),
∴∠B= ( )
∵∠B=∠D=37°(已知)
∴ =∠D (等量代换)
∴BC∥DE ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 在数学课上,老师提出如下问题:
已知:如图,四边形ABCD是平行四边形.求作:菱形AECF,使点E,F分别在BC,AD上.
小凯的作法如下:
(i)连接AC;
(ii)作AC的垂直平分线EF分别交BC,AD于E,F;
(iii)连接AE,CF.
所以四边形AECF是菱形.
老师说:“小凯的作法正确.”
请回答:在小凯的作法中,判定四边形AECF是菱形的依据是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角板是学习数学的重要工具,将一副三角板中的两块直角三角板的直角顶点![]() 按如图方式叠放在一起,当
按如图方式叠放在一起,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,解决下列问题:(友情提示:
的上方时,解决下列问题:(友情提示:![]() ,
,![]() ,
,![]() .
.

(1)①若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
②若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)这两块三角板是否存在一组边互相平行?若存在,请直接写出![]() 的角度所有可能的值(不必说明理由);若不存在,请说明理由.
的角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A +∠B=∠C;②∠A:∠B:∠C=l:2:3;③∠A=90°-∠B;④∠A=∠B=![]() ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个; B. 2个; C. 3个; D. 4个;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com