
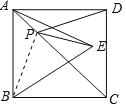
【题目】如图所示,正方形 ABCD 的面积为 16,△ABE 是等边三角形,点 E 在正方形 ABCD 内,在对角线 AC 上有一点 P,使 PD+PE 的和最小,则这个最小值为_____________ .

【答案】4
【解析】
先求得正方形的边长,依据等边三角形的定义可知 BE=AB=4,连结
BP,依据正方形的对称性可知 PB=PD,则 PE+PD=PE+BP.由两点之间线段最短可知:当点 B、P、E 在一条直线上时,PE+PD 有最小值,最小值为BE的长.
解:连结 BP.
∵四边形 ABCD 为正方形,面积为 16,
∴正方形的边长为 4.
∵△ABE 为等边三角形,
∴BE=AB=4.
∵四边形 ABCD 为正方形,
∴△ABP 与△ADP 关于 AC 对称.
∴BP=DP.
∴PE+PD=PE+BP.
由两点之间线段最短可知:当点 B、P、E 在一条直线上时,PE+PD 有最小值, 最小值=BE=4.
故答案为:4.


科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校合唱团有30名成员,下表是合唱团成员的年龄分布统计表:
年龄(单位:岁) | 13 | 14 | 15 | 16 |
频数(单位:名) | 5 | 15 | x | 10﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A.平均数、中位数
B.平均数、方差
C.众数、中位数
D.众数、方差
查看答案和解析>>
科目:初中数学 来源: 题型:
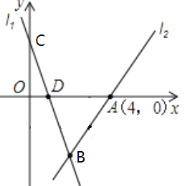
【题目】如图,直线l1:y=﹣3x+3交y轴于C,与x轴交于点D,直线l2经过点A(4,0),且直线l1、l2交于点B(2,m).
(1)求m的值和直线l2的函数表达式;
(2)直线l2在第一象限内的部分上有一点E,且△ADE的面积是△ADB面积的一半,求出点E的坐标,并在x轴上找一点P,使得CP+PE的值最小,求出这个最小值;
(3)若点Q为y轴上一点,且△BDQ为等腰三角形,请直接写出点Q的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车保有量是指一个地区拥有车辆的数量,一般是指在当地登记的车辆.进入21世纪以来,我国汽车保有量逐年增长.如图是根据中国产业信息网上的有关数据整理的统计图. 2007﹣2015年全国汽车保有量及增速统计图,
根据以上信息,回答下列问题:
(1)2016年汽车保有量净增2200万辆,为历史最高水平,2016年汽车的保有量为万辆,与2015年相比,2016年的增长率约为%;
(2)从2008年到2015年,年全国汽车保有量增速最快;
(3)预估2020年我国汽车保有量将达到万辆,预估理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
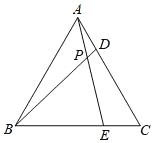
【题目】如图,△ABC 为等边三角形,D、E 分别是边 AC、BC 上的点,且AD=CE,AE 与 BD 相交于点 P.
(1)求∠BPE 的度数;
(2)若 BF⊥AE 于点 F,试判断 BP 与 PF 的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在△DBC 中,DB=DC,A 为△DBC 外一点,且∠BAC=∠BDC,DM⊥AC 于 M.
(1)求证:AD 平分△ABC 的外角;
(2)判断 AM、AC、AB 有怎样的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张三角形纸片ABC,其中∠C=90°,AC=6,BC=8.小静同学将纸片做两次折叠:第一次使点A落在C处,折痕记为m;然后将纸片展平做第二次折叠,使点A落在B处,折痕记为n.则m,n的大小关系是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
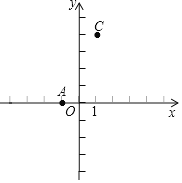
【题目】如图,![]() ,
,![]() ,点B在x轴上,且
,点B在x轴上,且![]() .
.
![]() 求点B的坐标;
求点B的坐标;
![]() 求
求![]() 的面积;
的面积;
![]() 在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com