
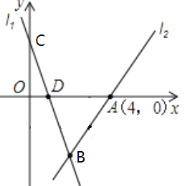
����Ŀ����ͼ��ֱ��l1��y=��3x+3��y����C����x�ύ�ڵ�D��ֱ��l2������A(4,0)����ֱ��l1��l2���ڵ�B(2,m����
��1����m��ֵ��ֱ��l2�ĺ�������ʽ��
��2��ֱ��l2�ڵ�һ�����ڵIJ�������һ��E���ҡ�ADE������ǡ�ADB�����һ�룬�����E�����꣬����x������һ��P��ʹ��CP+PE��ֵ��С����������Сֵ��
��3������QΪy����һ�㣬�ҡ�BDQΪ���������Σ���ֱ��д����Q�����ꣻ
���𰸡���1��m=-3��![]() ����2��E��5,1.5����
����2��E��5,1.5����![]() ����3��Q������Ϊ
����3��Q������Ϊ![]()
��������
��1������B(2,m������y=��3x+3��![]() m=
m=![]() ,�������ֱ��l2Ϊ
,�������ֱ��l2Ϊ![]()
��2�������D��1,0��,![]()
![]() ,��E������Ϊ
,��E������Ϊ![]() ��������ADE���������ADB�����һ�룬�������E��5,1.5�������ݶԳ�����������ͼ���ҵ�C����x��ĶԳƵ�C��,��ʱCP+PE=C,E��������֮����빫ʽ���������СֵΪC,E�ij�,
��������ADE���������ADB�����һ�룬�������E��5,1.5�������ݶԳ�����������ͼ���ҵ�C����x��ĶԳƵ�C��,��ʱCP+PE=C,E��������֮����빫ʽ���������СֵΪC,E�ij�,
��3���ֱ���B,DΪԲ��,BD��Ϊ�뾶����,�������y���ཻ��4������,�����BD���д�����y��Ľ���,�������������������ĵ�.
��1��![]() ��B(2,m����ֱ��l1��y=��3x+3�ϣ�
��B(2,m����ֱ��l1��y=��3x+3�ϣ�
![]() m=
m=![]()
��ֱ��l2�Ľ���ʽΪy=Kx+b
ֱ��l2������A(4,0)����B(2,-3����
![]()
![]()
���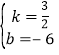
![]() ֱ��l2�Ľ���ʽΪ
ֱ��l2�Ľ���ʽΪ![]()
��2����y=0ʱ��0=-3x+3��x=1
![]() D��1,0��
D��1,0��
![]()
![]() ,
,
��E������Ϊ![]() ��
��
��![]()
a=5
![]() E��5,1.5��
E��5,1.5��
��C����x��ĶԳƵ�C��(0,-3),����C��E����x����P�㣬����CP������ͼ,
��ʱCP+EP����Сֵ����СֵΪC,E�ij�
![]()
��3��Q������Ϊ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
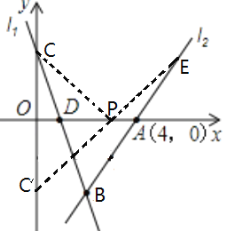
����Ŀ����ͼ����֪���ڡ�ABC�У���ACB��90�㣬CDΪ�ߣ���CD��CE���ȷ֡�ACB.
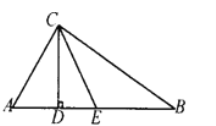
��1�����B�Ķ���.
��2����֤��CE��AB���ϵ����ߣ���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳���16����E�ڱ�AB�ϣ�AE=3������F�ڱ�BC�ϣ��Ҳ����B��C�غϣ�����EBF��EF�۵����õ���EB��F��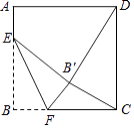
��1������BEF=45��ʱ����֤��CF=AE��
��2����B��D=B��Cʱ����BF�ij���
��3�����CB��F�ܳ�����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018���ɺ����ѧ������ɺ�д��Ķ����,Ϊ�˳�ʵƯ����ɲ���,����ȫУѧ������,�õ�����Ĵ���֧��.ͬʱ,����У���������꼶��Ҳ��������ʵѧУͼ����,�����꼶�鹺���˼ס���������Ȼ��ѧ�鼮���ɱ�,��ȥ8315Ԫ;��һ�꼶����A��B������ѧ�鼮���ɱ�,��ȥ6138Ԫ������A��B�������ֱ���ס��ҵ��������,�Ҽ�������B����ĵ�����ͬ,��������A����ĵ�����ͬ.��������ĵ��۱�������ĵ��۶�7Ԫ,������鼮�������鼮������_____________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����λ������ʮλ�ϵ������ǰ�λ�������λ���ֵĺͣ����dz������λ���С�ʥ�����������Ұ������ʥ��������ǰ��λ��ɵ���λ����Ϊm������λ��ɵ���λ����Ϊn�����涨d=![]() ����һ����λ��385��
����һ����λ��385��![]() 3+5=8��
3+5=8��![]() 385�ǡ�ʥ����������m=38��n=85����d=
385�ǡ�ʥ����������m=38��n=85����d=![]() =
=![]() .
.
��1��д����С�ġ�ʥ��������
��2����֤������һ����ʥ��������11�ı�����
��3����������ܱ�8�����ġ�ʥ����������ֱ��д����Щ��ʥ��������d����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E��50�㣬��BAC��50�㣬��D��110�������ABD�Ķ�����
�����ƽ����̣�������������д��Ӧ���������ݣ�
�⣺�ߡ�E��50�㣬��BAC��50��������֪��
���E���� ��������������
���� ������ �������� ����
���ABD+��D��180�㣮���� ����
���D��110��������֪��
���ABD��70��������ʽ�����ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������� ABCD �����Ϊ 16����ABE �ǵȱ������Σ��� E �������� ABCD �ڣ��ڶԽ��� AC ����һ�� P��ʹ PD+PE �ĺ���С���������СֵΪ_____________ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
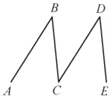
����Ŀ����ͼ�����AB��CD����B��37�㣬��D��37������ôBC��DEƽ���������������е���ջ���д���ɣ�
�⣺��AB��CD �� ��֪����
���B���� ������ ����
�ߡ�B����D��37������֪��
���� ������D ������������
��BC��DE ���� ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��DF����D+��B=180����

��1����֤��DE��BC��
��2�������AMD=75�������AGC�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com