
【题目】小明解方程 ![]() 的过程如图.请指出他解答过程中的错误步骤及错误原因,并写出正确的解答过程.
的过程如图.请指出他解答过程中的错误步骤及错误原因,并写出正确的解答过程.
解:方程两边同乘x得1﹣(x﹣2)=1.…①
去括号得1﹣x﹣2=1.…②
合并同类项得﹣x﹣1=1.…③
移项得﹣x=2.…④
解得x=﹣2.…⑤
所以原方程的解为x=﹣2.…⑥
【答案】解:步骤①去分母等号右边漏乘x;
步骤②去括号,当括号前是“﹣”的时候没有变号;
步骤⑥前少“检验”步骤,
正确解法:
方程两边同乘x,得1﹣(x﹣2)=x,
去括号,得1﹣x+2=x,
移项,得﹣x﹣x=﹣1﹣2,
合并同类项,得﹣2x=﹣3,
两边同除以﹣2,得x= ![]() ,
,
经检验,x= ![]() 是原方程的解,
是原方程的解,
∴原方程的解是x= ![]() .
.
【解析】步骤①去分母出错,等号右边漏乘x;步骤②去括号出错,当括号前是“﹣”的时候没有完全变号;步骤⑥前少“检验”步骤,正确的解法如下:方程两边同乘x,得1﹣(x﹣2)=x,去括号,得1﹣x+2=x,移项,得﹣x﹣x=﹣1﹣2,合并同类项,得﹣2x=﹣3,两边同除以﹣2,得x= ![]() ,
,
经检验,x= ![]() 是原方程的解,原方程的解是x=
是原方程的解,原方程的解是x= ![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知点C为线段AB延长线上的一点,以A为圆心,AC长为半径作⊙A,则点B与⊙A的位置关系为( )
A.点B在⊙A上B.点B在⊙A外C.点B在⊙A内D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一条直线的平行线有且只有一条
B.经过一点有且只有一条直线与已知直线平行
C.经过一点有两条直线与已知直线平行
D.过直线外一点有且只有一条直线与已知直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答下列问题.
例:当a>0时,如a=6,则|a|=|6|=6,故此时|a|是它本身;当a=0时,|a|=0,故此时|a|是零;
当a<0时,如a=﹣6,则|a|=|﹣6|=6=﹣(﹣6),故此时|a|是它的相反数.
综上所述,|a|可分三种情况,即|a|= 
这种分析方法渗透了数学的分类讨论思想.
问:
(1)请仿照例中的分类讨论的方法,分析二次根式 ![]() 的各种展开的情况.
的各种展开的情况.
(2)猜想 ![]() 与|a|的大小关系是
与|a|的大小关系是 ![]() |a|.
|a|.
(3)当1<x<2时,试化简: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块三角形玻璃损坏后,只剩下如图所示的残片,对图中的哪些数据测量后就可到建材部门割取符合规格的三角形玻璃( )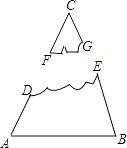
A.∠A,∠B,∠C
B.∠A,线段AB,∠B
C.∠A,∠C,线段AB
D.∠B,∠C,线段AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过(﹣2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0.其中正确结论的个数是( )
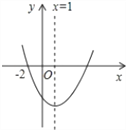
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,D、E分别是AB,AC上的点,AB=AC,AD=AE,然后将△ADE绕点A顺时针旋转一定角度,连接BD,CE,得到图②,将BD,CE分别延长至M,N,使DM= ![]() BD,EN=
BD,EN= ![]() CE,连接AM,AN,MN得到图③,请解答下列问题:
CE,连接AM,AN,MN得到图③,请解答下列问题: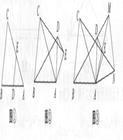
(1)在图②中,BD与CE的数量关系是;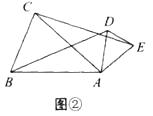
(2)在图③中,猜想AM与AN的数量关系,∠MAN与∠BAC的数量关系,并证明你的猜想.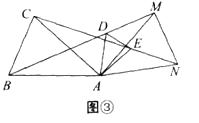
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com