
【题目】如图①,在△ABC中,D、E分别是AB,AC上的点,AB=AC,AD=AE,然后将△ADE绕点A顺时针旋转一定角度,连接BD,CE,得到图②,将BD,CE分别延长至M,N,使DM= ![]() BD,EN=
BD,EN= ![]() CE,连接AM,AN,MN得到图③,请解答下列问题:
CE,连接AM,AN,MN得到图③,请解答下列问题: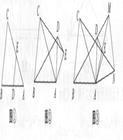
(1)在图②中,BD与CE的数量关系是;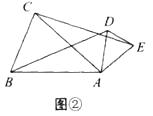
(2)在图③中,猜想AM与AN的数量关系,∠MAN与∠BAC的数量关系,并证明你的猜想.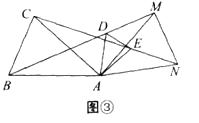
【答案】
(1)BD=CE
(2)解:AM=AN,∠MAN=∠BAC
∵ ∠DAE=∠BAC
∴ ∠CAE=∠BAD
在△BAD和△CAE中,
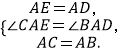
∴ △CAE≌△BAD(SAS)
∴ ∠ACE=∠ABD ,CE=BD
∵ DM= ![]() BD,EN=
BD,EN= ![]() CE,BD=CE,
CE,BD=CE,
∴ BM=CN
在△ABM和△ACN中,

∴ △ABM≌△ACN(SAS)
∴ AM=AN, ∠BAM=∠CAN,∴∠MAN=∠BAC.
【解析】(1)BD=CE,理由如下:由旋转的性质可知![]() BAD=
BAD=![]() CAE,又因AB=AC,AD=AE,由SAS判断出△BAD
CAE,又因AB=AC,AD=AE,由SAS判断出△BAD![]() △CAE,根据全等三角形对应边相等得出结论;
△CAE,根据全等三角形对应边相等得出结论;
(2)首先由SAS判断出△CAE≌△BAD,由全等三角形的性质得出 ∠ACE=∠ABD,CE=BD,从而得出 BM=CN,然后由SAS判断出 △ABM≌△ACN,根据全等三角形的性质得出 AM=AN, ∠BAM=∠CAN,从而得出即∠MAN=∠BAC.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】小明解方程 ![]() 的过程如图.请指出他解答过程中的错误步骤及错误原因,并写出正确的解答过程.
的过程如图.请指出他解答过程中的错误步骤及错误原因,并写出正确的解答过程.
解:方程两边同乘x得1﹣(x﹣2)=1.…①
去括号得1﹣x﹣2=1.…②
合并同类项得﹣x﹣1=1.…③
移项得﹣x=2.…④
解得x=﹣2.…⑤
所以原方程的解为x=﹣2.…⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P从点A出发,沿AB 运动到点B停止.过点E作EF⊥PE交射线BC于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
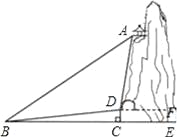
【题目】某旅游区有一个景观奇异的望天洞,D点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处.在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过D点作地面BE的垂线,垂足为C.
(1)求∠ADB的度数;(2)求索道AB的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.
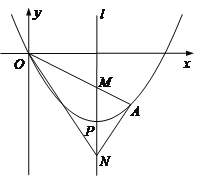
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
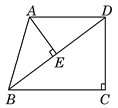
【题目】如图,已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强与小刚两位同学在学习“概率”时,做抛骰子(均匀立方体形状)试验,他们共抛了54次,出现不同向上点数的次数如下表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 6 | 9 | 5 | 8 | 16 | 10 |
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
(2)小强说:“根据试验,一次试验中出现向上点数为5的概率最大.”小刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断小强和小刚说法的对错.
(3)如果小强与小刚各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、C在BF上,AC∥DE,∠A=∠E,BD=CF, 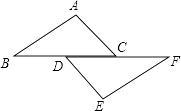
(1)求证:AB=EF.
(2)连接AF,BE,猜想四边形ABEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com