
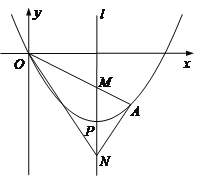
【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
【答案】(1)![]()
(2)12
(3)相似三角形的基本知识推出该角度的相等,不能
【解析】试题分析:(1)∵二次函数图象的顶点为P(4,-4),∴设二次函数的关系式为![]() 。
。
又∵二次函数图象经过原点(0,0),∴![]() ,解得
,解得![]() 。
。
∴二次函数的关系式为![]() ,即
,即![]() 。(2分)
。(2分)
(2)设直线OA的解析式为![]() ,将A(6,-3)代入得
,将A(6,-3)代入得![]() ,解得
,解得![]() 。
。
∴直线OA的解析式为![]() 。
。
把x=4代入![]() 得y=-2。∴M(4,-2)。
得y=-2。∴M(4,-2)。
又∵点M、N关于点P对称,∴N(4,-6),MN=4。
∴![]() 。(3分)
。(3分)
(3)①证明:过点A作AH⊥![]() 于点H,,
于点H,, ![]() 与x轴交于点D。则
与x轴交于点D。则
设A(![]() ),
),
则直线OA的解析式为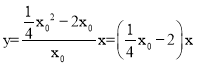 。
。
则M(![]() ),N(
),N(![]() ),H(
),H(![]() )。
)。
∴OD=4,ND=![]() ,HA=
,HA=![]() ,NH=
,NH=![]() 。
。
∴ 。
。
∴![]()
![]() 。∴∠ANM=∠ONM。(2分)
。∴∠ANM=∠ONM。(2分)
②不能。理由如下:分三种情况讨论:
情况1,若∠ONA是直角,由①,得∠ANM=∠ONM=450,
∴△AHN是等腰直角三角形。∴HA=NH,即![]() 。
。
整理,得![]() ,解得
,解得![]() 。
。
∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
情况2,若∠AON是直角,则![]() 。
。
∵![]() ,
,
∴![]() 。
。
整理,得![]() ,解得
,解得![]() ,
, ![]() 。
。
∴此时,故点A与原点或与点P重合。故此时不存在点A,使∠AON是直角。
情况3,若∠NAO是直角,则△AMN∽△DMO∽△DON,∴![]() 。
。
∵OD=4,MD=![]() ,ND=
,ND=![]() ,∴
,∴![]() 。
。
整理,得![]() ,解得
,解得![]() 。
。
∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
综上所述,当点A在对称轴![]() 右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)
右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)


科目:初中数学 来源: 题型:
【题目】阅读材料,解答下列问题.
例:当a>0时,如a=6,则|a|=|6|=6,故此时|a|是它本身;当a=0时,|a|=0,故此时|a|是零;
当a<0时,如a=﹣6,则|a|=|﹣6|=6=﹣(﹣6),故此时|a|是它的相反数.
综上所述,|a|可分三种情况,即|a|= 
这种分析方法渗透了数学的分类讨论思想.
问:
(1)请仿照例中的分类讨论的方法,分析二次根式 ![]() 的各种展开的情况.
的各种展开的情况.
(2)猜想 ![]() 与|a|的大小关系是
与|a|的大小关系是 ![]() |a|.
|a|.
(3)当1<x<2时,试化简: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=kx-1(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标.
(3)P为线段AB上一动点(P不与A、B重合),在(2)的情况下,直线y=ax﹣1与线段AB交于点P,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,D、E分别是AB,AC上的点,AB=AC,AD=AE,然后将△ADE绕点A顺时针旋转一定角度,连接BD,CE,得到图②,将BD,CE分别延长至M,N,使DM= ![]() BD,EN=
BD,EN= ![]() CE,连接AM,AN,MN得到图③,请解答下列问题:
CE,连接AM,AN,MN得到图③,请解答下列问题: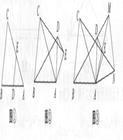
(1)在图②中,BD与CE的数量关系是;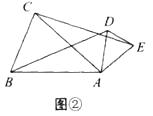
(2)在图③中,猜想AM与AN的数量关系,∠MAN与∠BAC的数量关系,并证明你的猜想.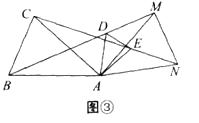
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,动点P从A点出发沿折线AD﹣DC﹣CB运动,当点P运动到点B时停止.已知动点P在AD、BC上的运动速度为1cm/s,在DC上的运动速度为2cm/s.△PAB的面积y(cm2)与动点P的运动时间t(s)的函数关系图象如图②.


(1)a=______,b=______;
(2)用文字说明点N坐标的实际意义;
(3)当t为何值时,y的值为2cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:

(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)问题情景:某学校数学学习小组在讨论“随机掷二枚均匀的硬币,得到一正一反的概率是多少”时,小聪说:随机掷二枚均匀的硬币,可以有“二正、一正一反、二反”三种情况,所以,P(一正一反)=![]() ;小颖反驳道:这里的“一正一反”实际上含有“一正一反,一反一正”二种情况,所以P(一正一反)=
;小颖反驳道:这里的“一正一反”实际上含有“一正一反,一反一正”二种情况,所以P(一正一反)=![]() .
.
⑴ 的说法是正确的.
⑵为验证二人的猜想是否正确,小聪与小颖各做了100次实验,得到如下数据:

计算:小聪与小颖二人得到的“一正一反”的频率分别是多少?从他们的实验中,你能得
到“一正一反”的概率是多少吗?
⑶对概率的研究而言小聪与小颖两位同学的实验说明了什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com