
【题目】阅读材料,解答下列问题.
例:当a>0时,如a=6,则|a|=|6|=6,故此时|a|是它本身;当a=0时,|a|=0,故此时|a|是零;
当a<0时,如a=﹣6,则|a|=|﹣6|=6=﹣(﹣6),故此时|a|是它的相反数.
综上所述,|a|可分三种情况,即|a|= 
这种分析方法渗透了数学的分类讨论思想.
问:
(1)请仿照例中的分类讨论的方法,分析二次根式 ![]() 的各种展开的情况.
的各种展开的情况.
(2)猜想 ![]() 与|a|的大小关系是
与|a|的大小关系是 ![]() |a|.
|a|.
(3)当1<x<2时,试化简: ![]() .
.
【答案】
(1)解:当a>0时,如a=3,则 ![]() ,故此时
,故此时 ![]() 的结果是它本身;
的结果是它本身;
当a=0时, ![]() =0,故此时
=0,故此时 ![]() 的结果是零;
的结果是零;
当a<0时,如a=﹣3,则 ![]() ,故此时
,故此时 ![]() 的结果是它的相反数.
的结果是它的相反数.
综上所述, ![]() 的结果可分三种情况,即
的结果可分三种情况,即 
(2)=
(3)解:∵1<x<2,
∴x﹣1>0,x﹣2<0,
∴ ![]() =x﹣1+(2﹣x)
=x﹣1+(2﹣x)
=1.
【解析】(1)根据算术平方根的非负性知![]()
![]() 0,故一个正数的平方的算术平方根等于它本身;0的平方的算术平方根等于它本身;一个负数的平方的算术平方根等于它的相反数;
0,故一个正数的平方的算术平方根等于它本身;0的平方的算术平方根等于它本身;一个负数的平方的算术平方根等于它的相反数;
(2)根据绝对值的非负性知:一个正数的绝对值等于它本身,零的绝对值等于零,负数的绝对值等于它的相反数;根据算术平方根的非负性知:一个正数的平方的算术平方根等于它本身;0的平方的算术平方根等于它本身;一个负数的平方的算术平方根等于它的相反数;故![]() =|a|;
=|a|;
(3)因1<x<2,故x﹣1>0,x﹣2<0根据绝对值及算数平方根的意义,分别化简,再合并即可。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第![]() 个图中正方形和等边三角形的个数之和为 个.
个图中正方形和等边三角形的个数之和为 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作∠A′O′B′=∠AOB
已知:∠AOB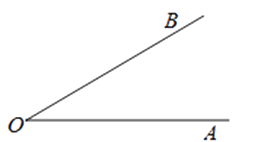
求作:∠A′O′B′=∠AOB
小米的作法如下:
① 作射线O′A′
② 以O为圆心,任意长为半径作弧,交OA于点C,交OB于点D
③ 以O′为圆心,OC为半径作弧C′E′,交O′A′于点C,
④ 以C′为圆心,CD为半径作弧,交C′E′于点D′
⑤ 过点D′做射线O′B′所以∠A′O′B′就是所求的角
如图: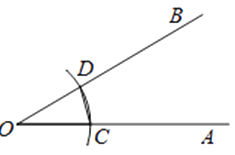
请回答:小米的作图依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程 ![]() 的过程如图.请指出他解答过程中的错误步骤及错误原因,并写出正确的解答过程.
的过程如图.请指出他解答过程中的错误步骤及错误原因,并写出正确的解答过程.
解:方程两边同乘x得1﹣(x﹣2)=1.…①
去括号得1﹣x﹣2=1.…②
合并同类项得﹣x﹣1=1.…③
移项得﹣x=2.…④
解得x=﹣2.…⑤
所以原方程的解为x=﹣2.…⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,有两个全等的直角三角形△ABC和△EDF,∠ACB=∠F=90°,∠A=∠E=30°,点D在边AB上,且AD=BD=CD.△EDF绕着点D旋转,边DE,DF分别交边AC于点M,K.
(1)如图2、图3,当∠CDF=0°或60°时,AM+CKMK(填“>”,“<”或“=”),你的依据是;

(2)如图4,当∠CDF=30°时,AM+CKMK(填“>”或“<”);
(3)猜想:如图1,当0°<∠CDF<60°时,AM+CKMK,试证明你的猜想..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.
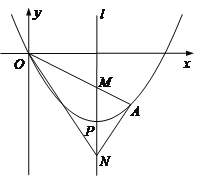
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com