[题目]在一张比例尺为1:2000的学校平面图上.操场的长度为4cm.则此操场的实际长度为 m．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】在一张比例尺为1:2000的学校平面图上，操场的长度为4cm，则此操场的实际长度为

______________m．

【答案】80

【解析】

根据比例尺＝图上距离：实际距离，列比例式即可求得实际长度．要注意统一单位．

解：设此操场的实际长度为x，
1：2000＝4：x，
解得：x＝8000cm＝80m．
∴此操场的实际长度为80m．
故答案为：80．

练习册系列答案

中学生英语随堂演练及单元要点检测题系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】命题“垂直于同一条直线的两条直线互相平行”的条件是（）

A. 如果两条直线垂直于同一条直线 B. 两条直线互相平行

C. 两条直线互相垂直 D. 两条直线垂直于同一条直线

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】阅读材料，解答下列问题．
例：当a＞0时，如a=6，则|a|=|6|=6，故此时|a|是它本身；当a=0时，|a|=0，故此时|a|是零；
当a＜0时，如a=﹣6，则|a|=|﹣6|=6=﹣（﹣6），故此时|a|是它的相反数．
综上所述，|a|可分三种情况，即|a|=
这种分析方法渗透了数学的分类讨论思想．
问：
（1）请仿照例中的分类讨论的方法，分析二次根式的各种展开的情况．
（2）猜想与|a|的大小关系是 |a|．
（3）当1＜x＜2时，试化简：．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】阅读下面材料：
在数学课上，老师提出如下问题：∠AOB
尺规作图：做一个角等于已知角
已知：∠AOB
求做：一个角，使它等于∠AOB

小强的作法如下：
① 作射线O′A'
② 以O为圆心，任意长为半径作弧，交OA于C,交OB于D
③ 以O′为圆心，OC为半径作弧C′E′, 交弧O′A′于C′
④ 以C′为圆心，CD为半径作弧, 交弧C′E′于D′
⑤过点D′作射线O′B′
所以∠A′O′B′就是所求的角

老师说：“小强的作法正确．”
请回答：小强用直尺和圆规作图∠A′O′B′=∠AOB，根据三角形全等的判定方法中的，
得出△D′O′C′≌△DOC，才能证明∠A′O′B′=∠AOB．

查看答案和解析>>

科目：初中数学 来源： 题型：

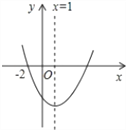
【题目】如图，二次函数y=ax2+bx+c（a≠0）的图象过（﹣2，0），则下列结论：①bc＞0；②b+2a=0；③a+c＞b；④16a+4b+c=0；⑤3a+c＜0.其中正确结论的个数是( )

A. 5 B. 4 C. 3 D. 2

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】请阅读下列材料：
问题：如图1，点A，B在直线l的同侧，在直线l上找一点P，使得AP+BP的值最小．
小明的思路是：如图2所示，先作点A关于直线l的对称点A′，使点A′，B分别位于直线l的两侧，再连接A′B，根据“两点之间线段最短”可知A′B与直线l的交点P即为所求．
请你参考小明同学的思路，探究并解决下列问题：

（1）如图3，在图2的基础上，设AA'与直线l的交点为C，过点B作BD⊥l，垂足为D．若CP=1，AC=1，PD=2，直接写出AP+BP的值；
（2）将（1）中的条件“AC=1”去掉，换成“BD=4﹣AC”，其它条件不变，直接写出此时AP+BP的值；
（3）请结合图形，求的最小值．