
【题目】请阅读下列材料:
问题:如图1,点A,B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小.
小明的思路是:如图2所示,先作点A关于直线l的对称点A′,使点A′,B分别位于直线l的两侧,再连接A′B,根据“两点之间线段最短”可知A′B与直线l的交点P即为所求.
请你参考小明同学的思路,探究并解决下列问题:
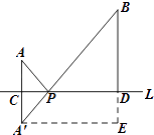
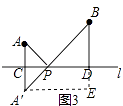
(1)如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D.若CP=1,AC=1,PD=2,直接写出AP+BP的值;
(2)将(1)中的条件“AC=1”去掉,换成“BD=4﹣AC”,其它条件不变,直接写出此时AP+BP的值;
(3)请结合图形,求 ![]() 的最小值.
的最小值.
【答案】
(1)解:如图2,∵AA′⊥l,AC=1,PC=1,
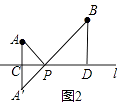
∴PA= ![]() ,
,
∴PA′=PA= ![]() ,
,
∵AA′∥BD,
∴∠A′=∠B,
∵∠A′PC=∠BPD,
∴△A′PC∽△BPD,
∴ ![]() ,
,
∴ ![]() ,
,
∴PB=2 ![]() ,
,
∴AP+PB= ![]() +2
+2 ![]() =3
=3 ![]() ;
;
故答案为3 ![]() ;
;
(2)解:作AE∥l,交BD的延长线于E,如图3,
则四边形A′EDC是矩形,
∴AE=DC=PC+PD=3,DE=A′C=AC,
∵BD=4﹣AC,
∴BD+AC=BD+DE=4,
即BE=4,
在RT△A′BE中,A′B= ![]() =5,
=5,
∴AP+BP=5,
故答案为5;
(3)解:设AC=1,CP=m﹣3,
∵A A′⊥L于点C,
∴AP= ![]() ,
,
设BD=2,DP=9﹣m,
∵BD⊥L于点D,
∴BP= ![]() ,
,
∴ ![]() 的最小值即为A′B的长.
的最小值即为A′B的长.
即:A′B= ![]() 的最小值.
的最小值.
如图,过A′作A′E⊥BD的延长线于点E.
∵A′E=CD=CP+PD=m﹣3+9﹣m=6,BE=BD+DE=2+1=3,
∴A′B= ![]() 的最小值
的最小值
= ![]()
= ![]() ,
,
∴ ![]() 的最小值为
的最小值为 ![]() .
.
【解析】 (1)根据等腰直角三角形知PA= ![]() ,根据轴对称性知PA′=PA,根据平行线的性质知∠A′=∠B,又∠A′PC=∠BPD,从而判断出△A′PC∽△BPD,根据相似三角形对应边成比例就可以求出PB的长,从而算出AP+BP;
,根据轴对称性知PA′=PA,根据平行线的性质知∠A′=∠B,又∠A′PC=∠BPD,从而判断出△A′PC∽△BPD,根据相似三角形对应边成比例就可以求出PB的长,从而算出AP+BP;
(2)作AE∥l,交BD的延长线于E,根据题意可以判断出四边形A′EDC是矩形,根据矩形的性质得出AE=DC=PC+PD=3,DE=A′C=AC,从而得出BD+AC=BD+DE=4,在RT△A′BE中,利用勾股定理算出A′B的长,从而得出AP+BP的值;
(1)设AC=1,CP=m﹣3,因A A′⊥L于点C,由勾股定理得出AP的值,设BD=2,DP=9﹣m,因BD⊥L于点D,由勾股定理得出BP的值,根据A′B=AP+BP的最小值,过A′作A′E⊥BD的延长线于点E.A′E=CD=CP+PD=m﹣3+9﹣m=6,BE=BD+DE=2+1=3,A′B=![]() ,从而得出答案。
,从而得出答案。


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,有两个全等的直角三角形△ABC和△EDF,∠ACB=∠F=90°,∠A=∠E=30°,点D在边AB上,且AD=BD=CD.△EDF绕着点D旋转,边DE,DF分别交边AC于点M,K.
(1)如图2、图3,当∠CDF=0°或60°时,AM+CKMK(填“>”,“<”或“=”),你的依据是;

(2)如图4,当∠CDF=30°时,AM+CKMK(填“>”或“<”);
(3)猜想:如图1,当0°<∠CDF<60°时,AM+CKMK,试证明你的猜想..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题的个数有( )
①带根号的数都是无理数; ②立方根等于它本身的数有两个,是0和1;
③0.01是0.1的算术平方根; ④有且只有一条直线与已知直线垂直
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=60°,∠ABC,∠ACB所对的边b,c满足:b ![]() +c
+c ![]() -4(b+c)+8=0.
-4(b+c)+8=0.
(1)证明:△ABC是边长为2的等边三角形.
(2)若 b,c两边上的中线BD,CE交于点O,求OD:OB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件为必然事件的是( )
A.小王参加本次数学考试,成绩是150分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,CCTV第一套节目正在播放新闻
D.口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com