
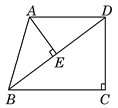
【题目】如图,已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
【答案】(1)证明见解析;(2)15.
【解析】试题分析:(1)由等腰三角形的性质可知∠ABD=∠ADB,由AD∥BC可知,∠ADB=∠DBC,由此可得∠ABD=∠DBC,又∵∠AEB=∠C=90°,利用“AA”可证△ABE∽△DBC;
(2)由等腰三角形的性质可知,BD=2BE,根据△ABE∽△DBC,利用相似比求BE,在Rt△ABE中,利用勾股定理求AE.
(1)证明:∵AB=AD=25,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC,
∵AE⊥BD,
∴∠AEB=∠C=90°,
∴△ABE∽△DBC;
(2)解:∵AB=AD,又AE⊥BD,
∴BE=DE,
∴BD=2BE,
由△ABE∽△DBC,
得![]() ,
,
∵AB=AD=25,BC=32,
∴![]() ,
,
∴BE=20,
∴AE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一块三角形玻璃损坏后,只剩下如图所示的残片,对图中的哪些数据测量后就可到建材部门割取符合规格的三角形玻璃( )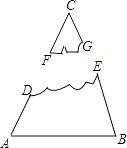
A.∠A,∠B,∠C
B.∠A,线段AB,∠B
C.∠A,∠C,线段AB
D.∠B,∠C,线段AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在函数y=kx(k>0)的图象上有三点A1(x1,y1),A2(x2,y2),A3(x3,y3),已知x1<x2<0<x3,则下列各式中正确的是( )
A. y1<y2<0<y3 B. y3<0<y1<y2
C. y2<y1<y3<0 D. y3<y1<0<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,D、E分别是AB,AC上的点,AB=AC,AD=AE,然后将△ADE绕点A顺时针旋转一定角度,连接BD,CE,得到图②,将BD,CE分别延长至M,N,使DM= ![]() BD,EN=
BD,EN= ![]() CE,连接AM,AN,MN得到图③,请解答下列问题:
CE,连接AM,AN,MN得到图③,请解答下列问题:
(1)在图②中,BD与CE的数量关系是;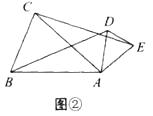
(2)在图③中,猜想AM与AN的数量关系,∠MAN与∠BAC的数量关系,并证明你的猜想.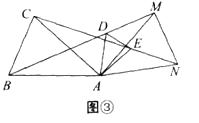
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:

(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=﹣3(x+1)2﹣2的图象与性质,下列说法正确的是( )
A.对称轴是直线x=1,最小值是﹣2
B.对称轴是直线x=1,最大值是﹣2
C.对称轴是直线x=﹣1,最小值是﹣2
D.对称轴是直线x=﹣1,最大值是﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0),点P是直线AB上的一个动点,记点P关于y轴对称的点为P′.
(1)当b=3时(如图1),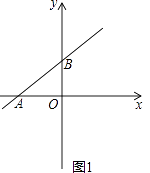
①求直线AB的函数表达式.
(2)②在x轴上找一点Q(点O除外),使△APQ与△AOB全等,直接写出点Q的所有坐标
(3)若点P在第一象限(如图2),设点P的横坐标为a,作PC⊥x轴于点C,连结AP′,CP′.当△ACP′是以点P′为直角顶点的等腰直角三角形时,求出a,b的值.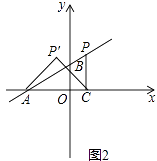
(4)当线段OP′恰好被直线AB垂直平分时(如图3),直接写出b= . 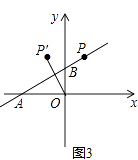
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①若a与c相交,则a与b相交;
②若a∥b,b∥c,那么a∥c;
③过一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
其中错误的有( )
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com