
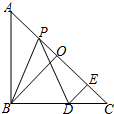
 如图,在△ABC中,∠ABC=90°,AB=BC,AC=2a,点O是AC的中点,点P是AC的任意一点,点D在BC边上,且满足PB=PD,作DE⊥AC于点E,设DE=x.
如图,在△ABC中,∠ABC=90°,AB=BC,AC=2a,点O是AC的中点,点P是AC的任意一点,点D在BC边上,且满足PB=PD,作DE⊥AC于点E,设DE=x.分析 (1)根据在等腰直角三角形ABC中,O是斜边AC的中点得到BO⊥AC,再根据DE⊥AC得到∠POB=∠DEP=90°,从而证明△POB≌△DEP,进而证得结论PE=BO;解时注意分P在AO上和P在OC上两种情况讨论;
(2)根据全等三角形的性质得到DE=OP=x,PE=OB=a,根据三角形的面积公式即可得到结论;
(3)根据AP•PC=(a-x)(a+x)=a2-x2,代入m=AP•PC+x2=a2,即可得到结论.
解答  解:(1)P在AO上,如图1:
解:(1)P在AO上,如图1:
∵在等腰直角三角形ABC中,O是斜边AC的中点,
∴BO⊥AC,
∵DE⊥AC,
∴∠POB=∠DEP=90°,
∵PB=PD,
∴∠PBD=∠PDB,
∵∠OBC=∠C=45°,
∴∠OBP+∠OBC=∠PDB=∠CPD+∠PCD,
∵∠PBD=∠PDB,
∴∠PB0=∠DPE,
在△POB与△DEP中,$\left\{\begin{array}{l}{∠POB=∠DEP}\\{∠PBO=∠DPE}\\{PB=PD}\end{array}\right.$,
∴△POB≌△DEP(AAS),
∴PE=BO;
P在OC上,如图2,
同理PE=BO;
(2)∵△OBP≌△EPD,
∴DE=OP=x,PE=OB=a,
∴$y=\frac{1}{2}DE•PC=\frac{1}{2}x(a+x)=\frac{1}{2}ax+\frac{1}{2}{x^2}$;
(3)∵AP•PC=(a-x)(a+x)=a2-x2,
∴m=AP•PC+x2=a2,
即不论点P在什么位置,m的值都是a2.
点评 本题考查了等腰直角三角形的性质,全等三角形的判定及性质,是一道难度较大、综合性较强的综合题,解题时一定要仔细审题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
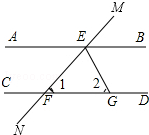 请补全说理过程:
请补全说理过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com