
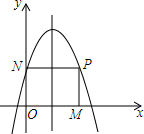 如图,抛物线的顶点坐标为(2,6),且经过点(4,2).P是抛物线上x轴上方一点,且在对称轴右侧,过点P作PM⊥x轴于点M,PN⊥y轴于点N.设点P横坐标为m.
如图,抛物线的顶点坐标为(2,6),且经过点(4,2).P是抛物线上x轴上方一点,且在对称轴右侧,过点P作PM⊥x轴于点M,PN⊥y轴于点N.设点P横坐标为m.分析 (1)根据待定系数法,可得答案;
(2)根据正方形的边长相等,可得关于m的方程,根据解方程,可得答案;
(3)根据矩形的周长公式,可得二次函数,根据二次函数的性质,可得答案;
(4)根据函数值相等两点关于对称轴对称,可得Q点的坐标,根据QN的长,可得不等式组,根据解不等式组,可得答案.
解答 解:(1)∵抛物线的顶点坐标为(2,6),
∴设抛物线对应的函数关系式为y=a(x-2)2+6.
∵抛物线经过点(4,2),
∴a(4-2)2+6=2,解得a=-1.
∴抛物线对应的函数关系式为y=-(x-2)2+6,即y=-x2+4x+2;
(2)∵点P在抛物线y=-x2+4x+2上,且点P的横坐标为m,
∴P点坐标为 P(m,-m2+4m+2).
当四边形OMPN为正方形时,PN=PM,
∴m=-m2+4m+2.
解得m1=$\frac{3+\sqrt{17}}{2}$,m2=$\frac{3-\sqrt{17}}{2}$ (舍去).
∵抛物线y=-x2+4x+2与x轴正半轴的交点为(2+$\sqrt{6}$,0),
且2<$\frac{3+\sqrt{17}}{2}$<2+$\sqrt{6}$,
∴m的值为$\frac{3+\sqrt{17}}{2}$.
(3)设四边形OMPN的周长为C,
C=2m+2(-m2+4m+2)=-2m2+10m+4=-2(m-$\frac{5}{2}$)2+$\frac{33}{2}$.
∵a=-2<0,2<$\frac{5}{2}$<2+$\sqrt{6}$,
∴当m=$\frac{5}{2}$时,四边形OMPN周长的最大值为$\frac{33}{2}$.
(4)如图 ,
,
点Q与点P(m,-m2+4m+2)关于x=2对称,得
Q(4-m,-m2+4m+2).
①当m<4时,由$\frac{1}{3}$≤QN≤1时,得
$\frac{1}{3}$≤4-m≤1,解得3≤m≤$\frac{11}{3}$;
②当m>4时,由$\frac{1}{3}$≤QN≤1时,得
$\frac{1}{3}$≤m-4≤1,解得,$\frac{13}{3}$≤m<2+$\sqrt{6}$;
综上所述,若直线PN与这条抛物线的另一个交点为点Q,直接写出$\frac{1}{3}$≤QN≤1时m的取值范围3≤m≤$\frac{11}{3}$或$\frac{13}{3}$≤m<2+$\sqrt{6}$.
点评 本题考查了二次函数综合题,把抛物线的解析式设为顶点式是解题关键;利用了正方形的性质;利用矩形的周长公式得出二次函数的解析是解题关键;利用函数值相等两点关于对称轴对称得出Q点的坐标是解题关键.


科目:初中数学 来源: 题型:填空题
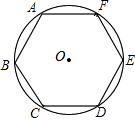 如图,正六边形ABCDEF内接于⊙O,向⊙O内任意投点,则所投的点落在正六边形ABCDEF内的概率是$\frac{3\sqrt{3}}{2π}$.
如图,正六边形ABCDEF内接于⊙O,向⊙O内任意投点,则所投的点落在正六边形ABCDEF内的概率是$\frac{3\sqrt{3}}{2π}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com