
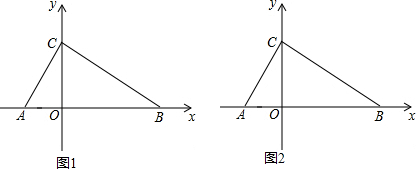
���� ��1����������AOC�У�����30�����Ե�ֱ�DZߵ���б�ߵ�һ�����AC�ij�����ֱ��������ABC�У�����30�����Ե�ֱ�DZߵ���б�ߵ�һ�����AB�ij�����AB-OA���OB�ij�������ȷ����B�����ꣻ
��2����ͼ1��ʾ����ֱ��������MCP�У�����30�����Ե�ֱ�DZߵ���б�ߵ�һ�룬��MP=t����ʾ��PC����ֱ��������QPC�У�����30�����Ե�ֱ�DZߵ���б�ߵ�һ���ʾ��PQ�����ɵó�d��t�Ĺ�ϵʽ��
��3����ͼ2��ʾ����E��GF��x�ᣬ��x���ڵ�F����PQ�ڵ�G����ֱ��������QCP�У�����30�����Ե�ֱ�DZߵ���б�ߵ�һ���ʾ��PC����AP-PC��ʾ��AC��������֪AC�ij����d��ֵ��ȷ����PC��PQ�ij�����ֱ��������PCB�У����ù��ɶ������PB�ij�����ΪPE�ij�����OF=GM=x����ʾ��GE����GF-EG��ʾ��EF����ֱ��������OEF�У����ù��ɶ����г�����x�ķ��̣�������̵Ľ�õ�x��ֵ��ȷ����OF=PC������OE=PB������HL�õ�ֱ��������OEF��ֱ��������PCBȫ�ȣ�����ȫ�������εĶ�Ӧ����ȵõ���EOF=��APB��������������ʼ��������APB-��OEB�Ķ�����
��� �⣺��1����Rt��AOC�У�OA=2����BAC=60�㣬
���ACO=30�㣬��AC=2OA=4��
��Rt��ABC�У���ABC=30�㣬
��AB=2AC=8����OB=AB-OA=8-2=6��
��B��6��0����
��2����ͼ1��ʾ��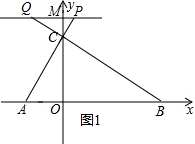
��Rt��MCP�У�MP=t����MCP=30�㣬
��CP=2MP=2t��
��Rt��CQP�У���CQP=30�㣬CP=2t��
��PQ=4t����d=4t��
��3����ͼ2��ʾ����E��GF��x�ᣬ��x���ڵ�F����PQ�ڵ�G��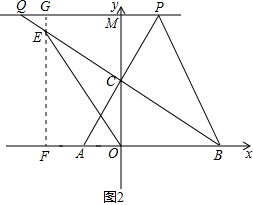
��Rt��PQC�У���CQP=30�㣬PQ=d��
��CP=$\frac{1}{2}$PQ=$\frac{1}{2}$d��
��AP=$\frac{5}{6}$d��
��AC=AP-CP=$\frac{1}{3}$d=4����d=12��
��PQ=12��PC=6��MP=3��QM=9��
��Rt��CBP��CP=6��BC=4$\sqrt{3}$��
��PB=$\sqrt{{6}^{2}+��4\sqrt{3}��^{2}}$=2$\sqrt{21}$��
��OE=PB=2$\sqrt{21}$��
��Rt��OEF����OF=GM=x��QG=9-x��
��Rt��QEG��GE=$\frac{\sqrt{3}}{3}$��9-x����
��MC=3$\sqrt{3}$��OC=2$\sqrt{3}$��
��GF=OM=5$\sqrt{3}$��
��EF=5$\sqrt{3}$-$\frac{\sqrt{3}}{3}$��9-x����
��Rt��OEF�У����ݹ��ɶ����ã�x2+[5$\sqrt{3}$-$\frac{\sqrt{3}}{3}$��9-x��]2=��2$\sqrt{21}$��2��
��ã�x=6��
��OF=PC=6��
��Rt��OEF��Rt��PBC��
$\left\{\begin{array}{l}{OE=PB}\\{OF=PC}\end{array}\right.$��
��Rt��OEF��Rt��PBC��HL����
���AOE=��APB��
�ߡ�AOE=��OEB+��ABC=��OEB+30�㣬����AOE-��OEB=30�㣬
���APB-��OEB=30�㣮
���� ��������һ�κ����ۺ��⣬�漰��֪ʶ�У���30��ֱ�������ε����ʣ�ȫ�������ε��ж������ʣ�������ʣ����ɶ�����������ͼ�����ʣ������������ʼ������ǽⱾ��Ĺؼ���


 �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 26 | B�� | 246 | C�� | 242 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
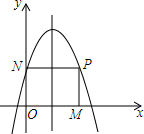 ��ͼ�������ߵĶ�������Ϊ��2��6�����Ҿ����㣨4��2����P����������x���Ϸ�һ�㣬���ڶԳ����Ҳ࣬����P��PM��x���ڵ�M��PN��y���ڵ�N�����P������Ϊm��
��ͼ�������ߵĶ�������Ϊ��2��6�����Ҿ����㣨4��2����P����������x���Ϸ�һ�㣬���ڶԳ����Ҳ࣬����P��PM��x���ڵ�M��PN��y���ڵ�N�����P������Ϊm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com