先化简，再求值：
，其中x是不等式组
的整数解．
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目：初中数学 来源： 题型：
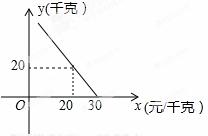
某超市对进货价为10元/千克的某种苹果的销售情况进行统计，发
现每天销售量y（千克）与销售价x（元/千克）存在一次函数关系，如图所示．
（1）求y关于x的函数关系式（不要求写出x的取值范围）；
（2）应怎样确定销售价，使该品种苹果的每天销售利润最大？最
大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
如右图，△ABC中，∠A=90°，点D在AC边上，DE∥BC，若
∠1=35°，则∠B的度数为 ( )
A．25° B．35° C．55° D．65°
查看答案和解析>>
科目：初中数学 来源： 题型：
某商场新近一批A、B两种型号的节能防近视台灯，每台进价分别为200元、170元，近两周的销售情况如下：
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第二周 | 4台 | 10台 | 3100元 |
（进价、售价均保持不变，利润=销售收入-进货成本）
(1)求A、B两种型号的台灯的销售单价；
(2)若该商场准备用不多于5400元的金额再购进这两种型号的台灯共30台，求A种型号的台灯最多能购进多少台？
(3)在(2)的条件下，该商场销售完这30台台灯能否实现利润为1400元的目标，若能，请给出相应的采购方案；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
如右图是交警在一个路口统计的某个时段来往辆的车速（单位：千米/时）情况，则这些车的车速的众数、中位数分别是
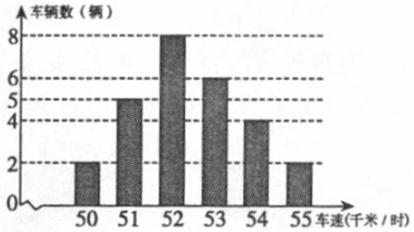
A. 8，6 B.8，5
C. 52，53 D.52，52
查看答案和解析>>
科目：初中数学 来源： 题型：
)阅读材料：如图1，在△AOB中，∠O=90°，OA=OB，点P在AB边上，PE⊥OA于点E，PF⊥OB于点F，则PE+PF=OA.（此结论不必证明，可直接应用）
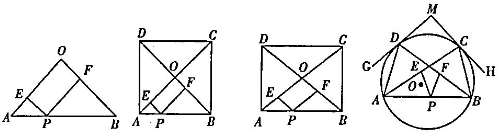图1 图2 图3 图4
(1)理解与应用
如图2，正方形ABCD的边长为2，对角线AC，BD相交于点O，点P在AB边上，PE⊥OA于点E，PF⊥OB于点F，则 PE+PF的值为_____________．
(2)类此与推理
如图3，矩形ABCD的对角线AC，BD相交于点O．AB=4，AD=3，点P在AB边上，PE
∥OB交AC于点E，PF∥OA交BD于点F，则PE+PF的值为______________．
(3)拓展与延伸
如图4，⊙○的半径为4，A，B，C，D是⊙○上的四点，过点C，D的切线CH，DG相交于点M，点P在弦AB上，PE∥BC交AC于点E，PF∥AD交BD于点F，当∠ADG=∠BCH=30°时，PE+PF是否为定值？若是，请求出这个定值；若不是，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
=x+1……4分
