
)阅读材料:如图1,在△AOB中,∠O=90°,OA=OB,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF=OA.(此结论不必证明,可直接应用)
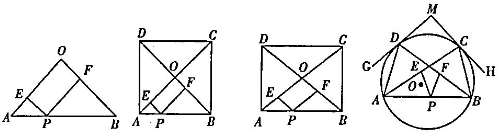 图1 图2 图3 图4
图1 图2 图3 图4
(1)理解与应用
如图2,正方形ABCD的边长为2,对角线AC,BD相交于点O,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则 PE+PF的值为_____________.
(2)类此与推理
如图3,矩形ABCD的对角线AC,BD相交于点O.AB=4,AD=3,点P在AB边上,PE
∥OB交AC于点E,PF∥OA交BD于点F,则PE+PF的值为______________.
(3)拓展与延伸
如图4,⊙○的半径为4,A,B,C,D是⊙○上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD交BD于点F,当∠ADG=∠BCH=30°时,PE+PF是否为定值?若是,请求出这个定值;若不是,请说明理由.
(1)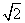 …………2分
…………2分
(2)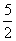 ……………… 4分
……………… 4分
(3)当∠ADG=∠BCH=30°时,PE+PF是定值,…………5分
理由:连接OA、OB、OC、OD,如图4.…………6分
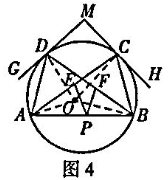
∵DG与⊙○相切,
∴∠GDA=∠ABD.
∵∠ADG=300,
∴∠ABD=30°
∴∠AOD=2∠ABD=60°.
∵OA= OD,
∴△AOD是等边三角形.………………………7分
∴AD=OA=4.
同理可得:BC=4.
∵PE∥BC,PF∥ AD,
∴△AEP∽△ACB,△BFP∽△BDA.………………8分
∴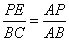 ,
,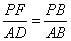 .
.
∴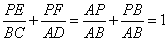 .………………9分
.………………9分
∴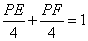 .
.
∴PE+PF=1,
∴当∠ADG=∠BCH=30°时,PE+PF=4.……………10分


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中的点,E、F分别是线段BM、CM的中点.
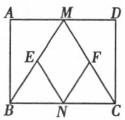
(1)求证:△ABM △DCM;
△DCM;
(2)当AB:AD为何值时,四边形MENF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为__________.
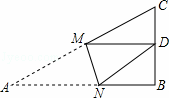
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com