
已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中的点,E、F分别是线段BM、CM的中点.
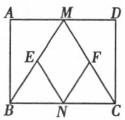
(1)求证:△ABM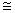 △DCM;
△DCM;
(2)当AB:AD为何值时,四边形MENF是正方形.
(1)证明: 四边形ABCD是矩形,
四边形ABCD是矩形,
 AB=DC,∠A=∠D=90°,…………………1分
AB=DC,∠A=∠D=90°,…………………1分
 M为AD的中点,
M为AD的中点, AM=DM,…………………………2分
AM=DM,…………………………2分
在△ABM和△DCM中
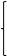 AM=DM
AM=DM
∠A=∠D
AB=DC
 △ABM
△ABM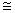 △DCM(SAS).…………………3分
△DCM(SAS).…………………3分
(2)当AB:AD=1:2时,四边形MENF是正方形,……………………4分
理由是: AB:AD=1:2,AM=DM,AB=CD,
AB:AD=1:2,AM=DM,AB=CD,
 AB-A=DM=DC,…………………………5分
AB-A=DM=DC,…………………………5分
 ∠A=∠D=90°,
∠A=∠D=90°,
 ∠ABM=∠AMB=∠DMC=∠DCM=45°,
∠ABM=∠AMB=∠DMC=∠DCM=45°,
 ∠BMC=90°………………6分
∠BMC=90°………………6分
 四边形ABCD是矩形,
四边形ABCD是矩形,
 ∠ABC=∠DCB=90°,
∠ABC=∠DCB=90°,
 ∠MBC= ∠MCB=45°,
∠MBC= ∠MCB=45°,
 BM=CM,………………………7分
BM=CM,………………………7分
 N、E、F分别是BC、BM、CM的中点,
N、E、F分别是BC、BM、CM的中点,
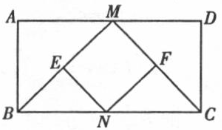
 BE=CF,ME=MF,NF∥BM,NE∥CM,
BE=CF,ME=MF,NF∥BM,NE∥CM,
 四边形AENF是平行四边形,…………………………8分
四边形AENF是平行四边形,…………………………8分
 AE=MF,∠BMC=90°,
AE=MF,∠BMC=90°,
 四边形MENF是正方形,
四边形MENF是正方形,
即当AB:AD=1:2时,四边形MENF是正方形。……………………9分


科目:初中数学 来源: 题型:
某市团委在2015年3月初组成了300个学雷锋小组,现从中随机抽取6个小组在3月份做好事件数的统计情况如图所示:
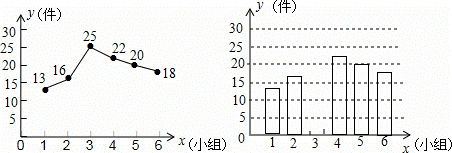
(1)这6个学雷锋小组在2015年3月份共做好事多少件?
(2)补全条形统计图;
(3)请估计该市300个学雷锋小组在2015年3月份共做好事多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
如右图是交警在一个路口统计的某个时段来往辆的车速(单位:千米/时)情况,则这些车的车速的众数、中位数分别是
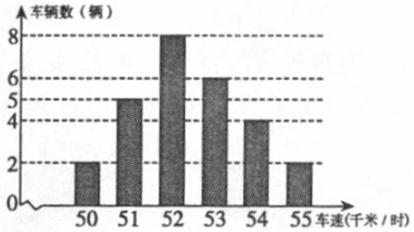
A. 8,6 B.8,5
C. 52,53 D.52,52
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,二次函数y=ax2 +bx+c(a>0)的图象的顶点为点D,其图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交于点C.在下面五个结论中:①2a -b=0;②a+b+c>o;③c=- 3a;④只有当a= 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有四个.其中正确的结论是_____________.(只填序号)
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有四个.其中正确的结论是_____________.(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
)阅读材料:如图1,在△AOB中,∠O=90°,OA=OB,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF=OA.(此结论不必证明,可直接应用)
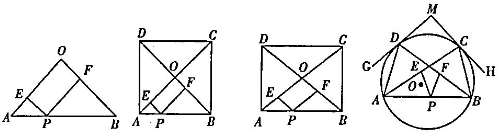 图1 图2 图3 图4
图1 图2 图3 图4
(1)理解与应用
如图2,正方形ABCD的边长为2,对角线AC,BD相交于点O,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则 PE+PF的值为_____________.
(2)类此与推理
如图3,矩形ABCD的对角线AC,BD相交于点O.AB=4,AD=3,点P在AB边上,PE
∥OB交AC于点E,PF∥OA交BD于点F,则PE+PF的值为______________.
(3)拓展与延伸
如图4,⊙○的半径为4,A,B,C,D是⊙○上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD交BD于点F,当∠ADG=∠BCH=30°时,PE+PF是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列球排列规律●○○ ●○○○○ ●○○ ●○○○○ ●○○●……从第一个到2015个球为止,共有●球( )个
A.501 B.502 C.503 D.504
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两人分别从相距72千米的A,B两地同时出发,相向而行。甲从A地出发,走了2千米时,发现有物品遗忘在A地,便立即返回,取了物品后立即从A地向B地行进,结果甲、乙两人恰好在AB的中点处相遇。若甲每时比乙多走1千米,求甲、乙两人的速度。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com