练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，二次函数y=ax2 +bx+c(a>0)的图象的顶点为点D，其图象与x轴的交点A、B的横坐标分别为-1，3，与y轴负半轴交于点C．在下面五个结论中：①2a -b=0；②a+b+c>o；③c=- 3a；④只有当a=时，△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有四个．其中正确的结论是_____________．（只填序号）

      


    ．③，④ 

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，以▱ABCO的顶点O为原点，边OC所在直线为x轴，建立平面直角坐标系，顶点A、C的坐标分别是（2，4）、（3，0），过点A的反比例函数y=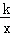的图象交BC于D，连接AD，则四边形AOCD的面积是　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


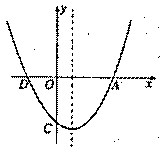
    如右图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x袖于点M，交y轴于点N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧在第二象限交于点P．若点P的坐标为(2a，b+1)，则a与b的数量关系为    (  )

      A．a-b        B．2a+b=-1  C．2a- b=l     D．2a+b=l

    查看答案和解析>>

    科目：初中数学 来源： 题型：


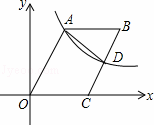
       如图，二次函数y=ax2+bx+c的图像与x轴的交点为A、D(A在D的右侧），与y轴的交点为C，且A(4，0)．C(0，-3)，对称轴是直线x=l． 

        (1)求二次函数的解析式； 

        (2)若M是第四象限抛物线上一动点，且横坐标为m，设四边形OCMA的面积为s．请写出s与m之间的函数关系式，并求出当m为何值时，四边形OCMA的面积最大；

        (3)设点B是x轴上的点，P是抛物线上的点，是否存在点P，使得以A，B、C，P四点为顶点的四边形为平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点P在以AB为直径的半圆内，连接AP、BP，并延长分别交半圆于点C、D，连接AD、BC并延长交于点F，作直线PF，下列说法一定正确的是

    ①     AC垂直平分BF；②AC平分∠BAF;③FP⊥AB；④BD⊥AF.

        A.①③    B.①④    C.②④    D.③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：如图，在矩形ABCD中，M、N分别是边AD、BC的中的点，E、F分别是线段BM、CM的中点．

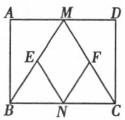
        (1)求证：△AB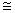M△DCM;

        (2)当AB：AD为何值时，四边形MENF是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，射线AB、AC被直线DE所截，则∠1与∠2是（      ）

    A.同旁内角                   B.内错角

    C.同位角                     D对顶角

    查看答案和解析>>

    科目：初中数学 来源： 题型：


       

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列各式计算正确的是

    A．     B．      C．     D．

    查看答案和解析>>

    同步练习册答案