
| 2 |
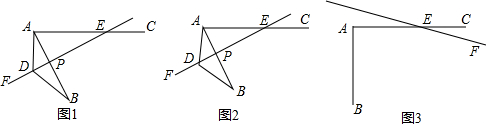
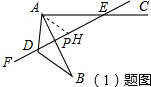 (1)证明:作∠DAH=∠EAB交DE于点H,
(1)证明:作∠DAH=∠EAB交DE于点H,
|
| α |
| 2 |
| α |
| 2 |
| 2 |
|
| 2 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
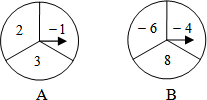 如图,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这6个数字.同时转动两个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A转盘中指针指向的数字记为x,B转盘中指针指向的数字记为y,且m=xy.
如图,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这6个数字.同时转动两个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A转盘中指针指向的数字记为x,B转盘中指针指向的数字记为y,且m=xy.查看答案和解析>>
科目:初中数学 来源: 题型:
| x2 |
| 4 |
| x2 |
| 4 |
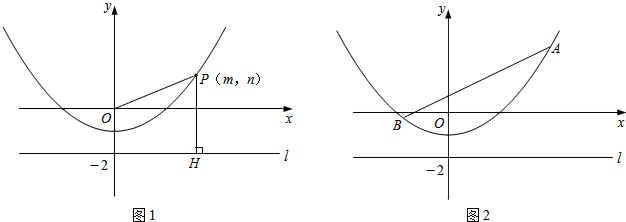
查看答案和解析>>
科目:初中数学 来源: 题型:
 初三学生小英、小亮为了解本校820名初二学生每周体育锻炼的情况,各自在本校进行了抽样调查.小英调查了初二年级体育爱好者中40名学生每周体育锻炼的时间,算得这些学生平均每周锻炼时间为7.5小时;小亮从全体初二学生名单中随机抽取了40名学生,调查了他们每周锻炼的时间,算得这些学生平均每周锻炼时间为5.8小时.小英与小亮整理各自样本数据,如表所示.请根据上述信息,回答下列问题:
初三学生小英、小亮为了解本校820名初二学生每周体育锻炼的情况,各自在本校进行了抽样调查.小英调查了初二年级体育爱好者中40名学生每周体育锻炼的时间,算得这些学生平均每周锻炼时间为7.5小时;小亮从全体初二学生名单中随机抽取了40名学生,调查了他们每周锻炼的时间,算得这些学生平均每周锻炼时间为5.8小时.小英与小亮整理各自样本数据,如表所示.请根据上述信息,回答下列问题:| 时间段(小时/周) | 小英抽样人数 | 小亮抽样人数 |
| 0-2 | 2 | 8 |
| 2-4 | 5 | 10 |
| 4-6 | 9 | 14 |
| 6-8 | 16 | 5 |
| 8-10 | 8 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com