
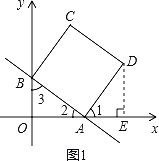
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.
x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.

(1)填空:b= ;
(2)求点D的坐标;
(3)点M是线段AB上的一个动点(点A、B除外),试探索在x上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.
【答案】(1)3;(2)(7,4);(3)存在,(﹣2,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)把(4,0)代入y=﹣![]() x+b即可求得b的值;
x+b即可求得b的值;
(2)过点D作DE⊥x轴于点E,证明![]() ,即可求得AE和DE的长,则D的坐标即可求得;
,即可求得AE和DE的长,则D的坐标即可求得;
(3)分当OM=MB=BN=NO时;当OB=BN=NM=MO=3时两种情况进行讨论.
解:(1)把(4,0)代入y=﹣![]() x+b,得:﹣3+b=0,解得:b=3,
x+b,得:﹣3+b=0,解得:b=3,
故答案是:3;
(2)如图1,过点D作DE⊥x轴于点E,
∵正方形ABCD中,∠BAD=90°,
∴∠1+∠2=90°,
又∵直角△OAB中,∠1+∠3=90°,
∴∠1=∠3,
在△OAB和△EDA中,
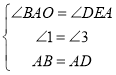
∴△OAB≌△EDA,
∴AE=OB=3,DE=OA=4,
∴OE=4+3=7,
∴点D的坐标为(7,4);
(3)存在.
①如图2,当OM=MB=BN=NM时,四边形OMBN为菱形.
则MN在OB的中垂线上,则M的纵坐标是![]() ,
,
把y=![]() 代入y=﹣
代入y=﹣![]() x+3中,得x=2,即M的坐标是(2,
x+3中,得x=2,即M的坐标是(2,![]() ),
),
则点N的坐标为(﹣2,![]() ).
).
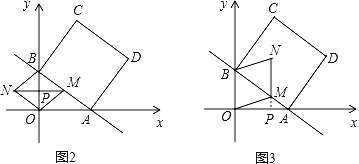
②如图3,当OB=BN=NM=MO=3时,四边形BOMN为菱形.
∵ON⊥BM,
∴ON的解析式是y=![]() x.
x.
根据题意得: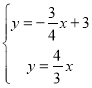
解得: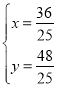
则点N的坐标为(![]()
综上所述,满足条件的点N的坐标为(﹣2,![]() )或(
)或(![]() .
.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,线段AC是⊙O的直径,过A点作直线BF交⊙O于A、B两点,过A点作∠FAC的角平分线交⊙O于D,过D作AF的垂线交AF于E.
(1)证明DE是⊙O的切线;
(2)证明AD2=2AEOA;
(3)若⊙O的直径为10,DE+AE=4,求AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】舍利生生塔位于晋祠南瑞,建于隋开皇年间,宋代重修,清乾隆十六年(1751年)重建.七屋八角,琉璃瓦顶,远远望去,高耸的古塔,映衬着蓝天白云,甚是壮观.原塔内每层均有佛像,开4门8窗,凭窗远眺,晋祠内外美景可一览无余.如果在夕阳西下时欣赏宝塔,还会出现——天云锦、满塔光辉的壮丽景观,被誉为“宝塔披霞”.某数学“综合与实践”小组的同学把“测量舍利生生塔高”作为一项课题活动,他们制定了测量方案,并利用课余时间完成了实地测量,测量结果如表:
课题 | 测量舍利生生塔高 | |||
测量示意图 |
| 说明:某同学在地面上选择点C,使用手持测角仪,测得此时楼顶A的仰角∠AHE=α,沿CB方向前进到点D,测量出C,D之间的距离CD=xm,在点D使用手持测角仪,测得此时楼顶A的仰角∠AFE=β | ||
测量数据 | α的度数 | β的度数 | CD的长度 | 该同学眼睛离地面的距离HC |
24° | 37° | 32m | 1.76m | |
… | … | |||
(1)请帮助该小组的同学根据上表中的测量数据,求塔高AB.(结果精确到1m;参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(2)该小组要写出一份完整的课题活动报告,除上表中的项目外,你认为还需要补充哪些项目?(写出一个即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=AC,点 M 在 BA 的延长线上,点 N 在 BC 的延长线上,过点 C 作CD∥AB 交∠CAM 的平分线于点 D.
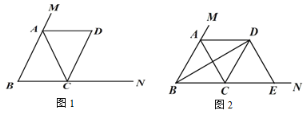
(1)如图 1,求证:四边形 ABCD 是平行四边形;
(2)如图 2,当∠ABC=60°时,连接 BD,过点 D 作 DE⊥BD,交 BN 于点 E,在不添加任何辅助线的情况下,请直接写出图 2 中四个三角形(不包含△CDE),使写出的每个三角形的面积与△CDE 的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,以点A为圆心AB长为半径画弧交AD于点F,再分别以点B,F为圆心,大于![]() BF的长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.
BF的长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.
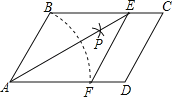
(1)求证:四边形ABEF是菱形;
(2)若∠C=60°,AE=4![]() ,求菱形ABEF的面积.
,求菱形ABEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线顶点;
为抛物线顶点;
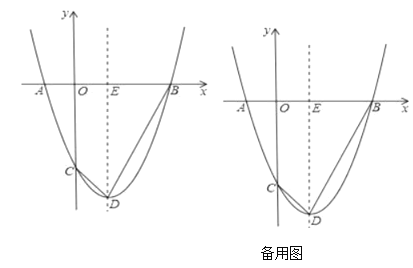
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)连结![]() 、
、![]() ,抛物线的对称轴与
,抛物线的对称轴与![]() 轴交于点
轴交于点![]() .
.
①若线段![]() 上有一点
上有一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
②若抛物线上一点![]() ,作
,作![]() ,交直线
,交直线![]() 于点
于点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了对该区八年级数学学科教学质量进行检查,对该区八年级的学生进行摸底,为了解摸底的情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:随机抽取![]() 学校与
学校与![]() 学校的各20名学生的数学成绩(单位:分)进行
学校的各20名学生的数学成绩(单位:分)进行
| 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
| 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据:按如下数据段整理、描述这两组数据
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
| 1 | 1 | 0 | 0 | 3 | 7 | 8 |
|
分析数据:两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
| 81.85 | 88 | 91 | 268.43 |
| 81.95 | 86 | m | 115.25 |
得出结论:
![]() :若
:若![]() 学校有800名八年级学生,估计这次考试成绩80分以上(包含80分)人数为多少人?
学校有800名八年级学生,估计这次考试成绩80分以上(包含80分)人数为多少人?
![]() :根据表格中的数据,推断出哪所学校学生的数学水平较高,并说明理由.(至少从两个不同的角度说明推断的合理性)
:根据表格中的数据,推断出哪所学校学生的数学水平较高,并说明理由.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com