
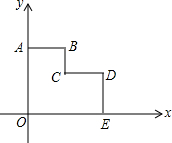
 如图,在平面直角坐标系xOy中,多边形OABCDE的顶点分别为O(0,0)、A(0,8)、B(4,8)、C(4,4)、D(8,4)、E(8,0),若直线l经过点M(3,$\frac{7}{2}$),分别与边OA、DE相交且将多边形OABCDE面积平分.
如图,在平面直角坐标系xOy中,多边形OABCDE的顶点分别为O(0,0)、A(0,8)、B(4,8)、C(4,4)、D(8,4)、E(8,0),若直线l经过点M(3,$\frac{7}{2}$),分别与边OA、DE相交且将多边形OABCDE面积平分.分析 (1)直线l将多边形分得的两部分当中,下面部分是一个梯形,只需让梯形的面积等于多边形面积的一半即可,由此设出直线l的解析式y=kx+b,求出直线与AO、DE的交点K、R,进而表示出梯形的面积,根据梯形面积等于多边形面积的一半列出方程,再加上直线l过点M,则可求k和b.
(2)要求出a的值,必然要找到关于a的方程,而a是二次函数的常数项,且直线l与抛物线相交于两点,由此联想到用韦达定理来解决问题.由于∠FOG=90°,因此可分别过F、G两点向x轴作垂线构造相似三角形,得线段比例关系,而线段是可以用F、G两点的坐标表示的,结合韦达定理,a自然解出.
(3)由于过N点要有无数条直线将多边形面积平分,那么只需要转动(1)当中的梯形的腰KR且保持梯形的面积不变即可,绕着转动的这个点N就是KR的中点,因为直线绕KR中点转动会出现全等三角形,也就是说梯OERK的面积减少的与增加的一样多,就始终等于多边形OABCDE面积的一半.
解答 解:(1)∵O(0,0)、A(0,8)、B(4,8)、C(4,4)、D(8,4)、E(8,0),
∴多边形OABCDE的面积为8×8-4×4=48,
设直线l的函数表达式为y=kx+b,
∵l过点M(3,$\frac{7}{2}$),
∴$\frac{7}{2}$=3k+b,①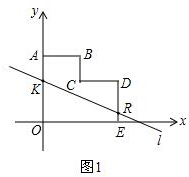
设直线l与DE交于点R,与AO交于点K,如图1,
则K(0,b),R(8,8k+b),
∴S梯FOEG=$\frac{1}{2}$(FO+GE)×OE=$\frac{1}{2}$(8k+b+b)×8=24,
∴4k+b=3,②
由①②可解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=5}\end{array}\right.$,
∴l的解析式为y=-$\frac{1}{2}$x+5,
K(0,5),R(8,1).
(2)∵直线l与抛物线y=x2+$\frac{1}{2}$x+a交于F、G两点,
故联立方程组$\left\{\begin{array}{l}{y=-\frac{1}{2}x+5}\\{y={x}^{2}+\frac{1}{2}x+a}\end{array}\right.$,
消去y整理得:x2+x+a-5=0,
设F(x1,y1),G(x2,y2),则$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=-1}\\{{x}_{1}•{x}_{2}=a-5}\end{array}\right.$,
∴${y}_{1}•{y}_{2}=(-\frac{1}{2}{x}_{1}+5)(-\frac{1}{2}{x}_{2}+5)$=$\frac{1}{4}{x}_{1}•{x}_{2}-\frac{5}{2}({x}_{1}+{x}_{2})+25$=$\frac{1}{4}a+\frac{105}{4}$,
过点F作FP⊥x轴于点P,过点G作GH⊥x轴于点H,如图2,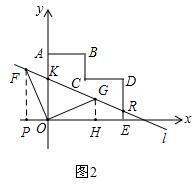
∵∠FOG=90°,
∴∠FOP+∠GOH=90°,
∵∠FOP+∠PFO=90°,
∴∠PFO=∠GOH,
∴△FOP∽△OGH,
∴$\frac{FP}{OH}=\frac{OP}{GH}$,
∴$\frac{{y}_{1}}{{x}_{2}}=\frac{-{x}_{1}}{{y}_{2}}$,
∴x1•x2+y1•y2=0,
∴$a-5+\frac{1}{4}a+\frac{105}{4}=0$,
解得:a=-17.
(3)取N为KR的中点即可,原因如下:
过点N作任意直线与AO交于点J,与DE交于点Q,如图3,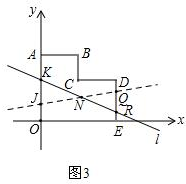
∵DE∥AO,
∴∠NKJ=∠NRQ,∠NJK=∠NQR,
在△KNJ与△RNQ中,
$\left\{\begin{array}{l}{∠NKJ=∠NRQ}\\{∠NJK=∠NQR}\\{NK=KR}\end{array}\right.$,
∴△KNJ≌△RNQ(AAS),
∴梯形OJQE与梯形OKRE的面积是相等的,
∵梯形OKRE的面积是多边形OABCDE面积的一半,
∴过N点有无数条直线将多边形OABCDE面积平分.
∵K(0,5),R(8,1),
∴N(4,3)即满足要求的点.
点评 本题考查了面积求法、待定系数法求一次函数解析式、韦达定理、直线与抛物线的位置关系、相似三角形的判定与性质、全等三角形的判定与性质、等积变换等多个知识点,综合性与技巧性都比较强,难度较大,是一道值得同学们研习的好题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
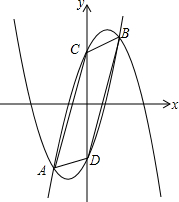 已知,如图,抛物线l1:y=-x2+2x+3与抛物线l2:y=x2+2x-3相交于点A,B,它们分别与y轴相交于C,D,其中点A的横坐标比点B的横坐标小.
已知,如图,抛物线l1:y=-x2+2x+3与抛物线l2:y=x2+2x-3相交于点A,B,它们分别与y轴相交于C,D,其中点A的横坐标比点B的横坐标小.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
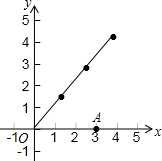 如图,在平面直角坐标系中,A点坐标为(3,0),线段OA绕原点O每次按逆时针方向旋转60°,并且每旋转一次长度增加两倍,例如:OA1=3OA,∠A1OA=60°,那么按照此规律,A2的坐标为(-$\frac{27}{2}$,$\frac{27\sqrt{3}}{2}$),A100的坐标为$(-\frac{{3}^{101}}{2},-\frac{{3}^{101}\sqrt{3}}{2})$.
如图,在平面直角坐标系中,A点坐标为(3,0),线段OA绕原点O每次按逆时针方向旋转60°,并且每旋转一次长度增加两倍,例如:OA1=3OA,∠A1OA=60°,那么按照此规律,A2的坐标为(-$\frac{27}{2}$,$\frac{27\sqrt{3}}{2}$),A100的坐标为$(-\frac{{3}^{101}}{2},-\frac{{3}^{101}\sqrt{3}}{2})$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com