
 一条河的两岸有一段是互相平行的,为了测量河宽,王刚先站在河边观察对岸的一目标B,然后在岸边做一标记D,使BD垂直于河岸,再沿河岸走到点C,接着垂直河岸走到点A,使A,B和岸边的一点F在一条直线上.如果量得AC=5m,FD=20m,CF=4m,那么河宽BD有多少米?
一条河的两岸有一段是互相平行的,为了测量河宽,王刚先站在河边观察对岸的一目标B,然后在岸边做一标记D,使BD垂直于河岸,再沿河岸走到点C,接着垂直河岸走到点A,使A,B和岸边的一点F在一条直线上.如果量得AC=5m,FD=20m,CF=4m,那么河宽BD有多少米? 科目:初中数学 来源: 题型:解答题
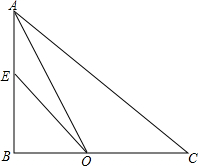 在△ABC中,∠ABC=90°,∠A的平分线AO交BC于O点,将线段OC绕点O逆时针旋转,使点C恰好落在边AB上E点处
在△ABC中,∠ABC=90°,∠A的平分线AO交BC于O点,将线段OC绕点O逆时针旋转,使点C恰好落在边AB上E点处 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
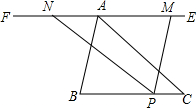 如图所示,P点是线段BC上的一点,过点A作EF∥BC,过点P分别作PM∥AB,PN∥AC,PM,PN分别交EF于M,N两点,当BP=2PC时.线段AM与AN有什么数量关系?为什么?
如图所示,P点是线段BC上的一点,过点A作EF∥BC,过点P分别作PM∥AB,PN∥AC,PM,PN分别交EF于M,N两点,当BP=2PC时.线段AM与AN有什么数量关系?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
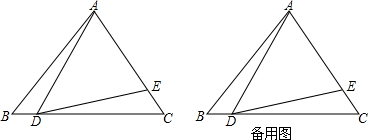
 如图,在⊙O中,AB,CD为圆的两条弦,CD与OA,OB分别交于点E,F,且$\widehat{AC}=\widehat{BD}$,求证:OE=OF.
如图,在⊙O中,AB,CD为圆的两条弦,CD与OA,OB分别交于点E,F,且$\widehat{AC}=\widehat{BD}$,求证:OE=OF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
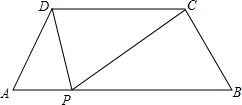 如图,梯形ABCD中,AB∥CD,AD=BC,∠A=60°,AD=4,CD=6,动点P从点A出发,沿AB方向以2单位长度/秒的速度向终点B运动,连接PC,PD,设点P运动的时间为t秒.
如图,梯形ABCD中,AB∥CD,AD=BC,∠A=60°,AD=4,CD=6,动点P从点A出发,沿AB方向以2单位长度/秒的速度向终点B运动,连接PC,PD,设点P运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
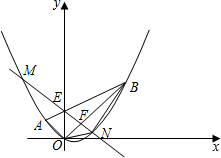 如图,平面直角坐标系xOy中,点A的坐标为(-2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连结OA、OB、AB,线段AB交y轴于点E.
如图,平面直角坐标系xOy中,点A的坐标为(-2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连结OA、OB、AB,线段AB交y轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 |
| 中国数字音乐销售额/亿元 | 15.2 | 16.5 | 17.9 | 19.5 | 21.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com