
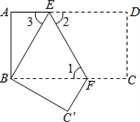
【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)若∠1=60°,求∠3的度数;
(2)求证:BE=BF
(3)若AB=6,AD=12,求△BEF的面积.
【答案】(1)60°;(2)证明见解析;(3)7.5
【解析】试题分析:(1)根据平行线的性质、翻转变换的性质解答;
(2)根据等腰三角形的性质证明;
(3)根据翻转变换的性质、勾股定理计算即可.
试题解析:(1)∵AD∥BC,
∴∠2=∠1=60°,
由翻转变换的性质可知,∠BEF=∠2=60°,
∴∠3=60°;
(2)证明:∵∠BEF=∠1=60°,
∴BE=BF;
(3)由翻转变换的性质可知,BE=DE=12-AE,
由勾股定理得,BE2=AB2+AE2,即(12-AE)2=62+AE2,
解得,AE=4.5,
则BF=BE=7.5,
∵四边形ABHE是矩形,
∴EH=AB=6,
∴△BEF的面积=![]() ×BF×EH=22.5.
×BF×EH=22.5.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】中秋节前夕,旺客隆超市采购了一批土特产,根据以往销售经验,每天的售价与销售量之间有如下表的关系:

设当售价从38元/千克下调到x元/千克时,销售量为y千克.
(1)根据上述表格中提供的数据,通过在直角坐标系中描点、连线等方法,猜测并求出y与x之间的函数表达式;
(2)如果这种土特产的成本价是20元/千克,为使某一天的利润为780元,那么这一天每千克的售价应为多少元?(利润=销售总金额-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k﹣3)x+k2+1=0有两个不相等的实数根x1、x2.
(1)求k的取值范围;
(2)若x1、x2满足|x1|+|x2|=2|x1x2|﹣3,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. 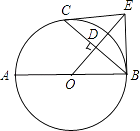
(1)求证:BE与⊙O相切;
(2)连接AD并延长交BE于点F,若OB=9,sin∠ABC= ![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果点P(x,y)的坐标满足x+y=xy,那么称P为和谐点.
(1)若点A(a,2)是正比例函数y=kx(k≠0,k为常数)上的一个和谐点,求这个正比例函数的解析式;
(2)试判断函数y=﹣2x+1的图象上是否存在和谐点?若存在,求出和谐点的坐标;若不存在,请说明理由;
(3)直线l:y=kx+2经过和谐点P,且与反比例函数G:y=﹣ ![]() 交于M、N两点,若点P的纵坐标为3,求出直线l的解析式,并在x轴上找一点Q使得QM+QN最小.
交于M、N两点,若点P的纵坐标为3,求出直线l的解析式,并在x轴上找一点Q使得QM+QN最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大双,小双的妈妈申购到一张北京奥运会的门票,兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球,各自设计一种游戏确定谁去.
大双:A袋中放着分别标有数字1,2,3的三个小球,B袋中放着分别标有数字4,5的两个小球,且都已各自搅匀,小双蒙上眼睛从两个口袋中各取出1个小球,若两个小球上的数字之积为偶数,则大双得到门票;若积为奇数,则小双得到门票.
小双:口袋中放着分别标有数字1,2,3的三个小球,且已搅匀,大双,小双各蒙上眼睛有放回地摸1次,大双摸到偶数就记2分,摸到奇数记0分;小双摸到奇数就记1分,摸到偶数记0分,积分多的就得到门票.(若积分相同,则重复第二次.)
(1)大双设计的游戏方案对双方是否公平?请你运用列表或树状图说明理由;
(2)小双设计的游戏方案对双方是否公平?不必说理.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com