Question

5．如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F．切点为G，连接AG交CD于K．
（1）如图1，求证：KE=GE；
（2）如图2，若AC∥EF，试判断线段KG、KD、GE间的数量关系，并说明理由；
（3）在（2）的条件下，若sinE=$\frac{3}{5}$，AK=2$\sqrt{3}$，求⊙O的半径．

Answer 1

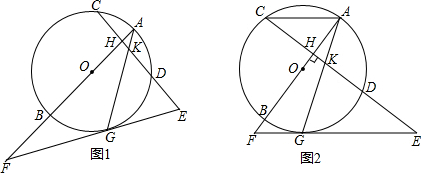
分析 （1）如图1，连接OG．根据切线性质及CD⊥AB，可以推出∠KGE=∠AKH=∠GKE，根据等角对等边得到KE=GE；
（2）如图2，根据平行得角相等，证明△GKD∽△EFG，列比例式可得结论；
（3）如图3所示，连接OG，OC，由（1）得KE=GE，根据sinE=$\frac{3}{5}$设AH=3t，则AC=5t，CH=4t，列式先求t的值，再求出圆的半径．

解答 解：（1）如图1，连接OG．
∵EG为切线，
∴∠KGE+∠OGA=90°，
∵CD⊥AB，
∴∠AKH+∠OAG=90°，
又∵OA=OG，
∴∠OGA=∠OAG，
∴∠KGE=∠AKH=∠GKE，
∴KE=GE．
（2）KG²=KD•GE，理由是：
连接GD，如图2，
∵AC∥EF，
∴∠C=∠E，
∵∠C=∠AGD，
∴∠E=∠AGD，
∵∠GKD=∠GKD，
∴△GKD∽△EKG，
∴$\frac{GK}{EK}=\frac{KD}{KG}$，
∴KG²=KD•EK，
由（1）得：EK=GE，
∴KG²=KD•GE； 
（3）连接OG，OC，如图3所示，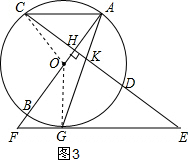
由（1）得：KE=GE．
∵AC∥EF
∴∠E=∠ACH
∵sinE=sin∠ACH=$\frac{3}{5}$，
设AH=3t，则AC=5t，CH=4t，
∵KE=GE，AC∥EF，
∴CK=AC=5t，
∴HK=CK-CH=t．
在Rt△AHK中，根据勾股定理得AH²+HK²=AK²，
即（3t）²+t²=$（2\sqrt{3}）^{2}$，解得t=$\frac{\sqrt{30}}{5}$．
设⊙O半径为r，在Rt△OCH中，OC=r，OH=r-3t，CH=4t，
由勾股定理得：OH²+CH²=OC²，
即（r-3t）²+（4t）²=r²，解得r=$\frac{25}{6}$t=$\frac{5\sqrt{30}}{6}$，
答：⊙O的半径为$\frac{5\sqrt{30}}{6}$．

点评 此题考查了切线的性质，相似三角形的判定与性质，垂径定理，勾股定理，锐角三角函数定义，圆周角定理，平行线的判定，以及等腰三角形的判定，熟练掌握定理及性质是解本题的关键．