
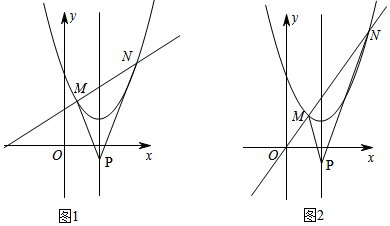
���� ��1���ٸ��ݵ�M��N�����꣬���ô���ϵ�������ɽ�����⣮
�ڲ���Q��3��6-t������ֱ��MN�Ľ���ʽ��y=kx+b��k��0������$\left\{\begin{array}{l}{y=kx+b}\\{y=\frac{1}{2}��x-3��^{2}+3}\end{array}\right.$��x2-��2k+6��x+15-2b=0�ɵ�xM+xN=2k+6��xM•xN=15-2b����tan��MPQ=tan��NPQ����$\frac{3-{x}_{M}}{{y}_{M}-t}$=$\frac{{x}_{N}-3}{{y}_{N}-t}$�������12k-2kb-2kt-6k2=0����Ϊk��0����6-b-t-3k=0������b=6-t-3k������y=kx+6-t-3k=k��x-3��+6-t���ɴ˼����ж�������Q��3��6-t����
��2�������⣬Q��3��9����ֱ��MN������0��0����Q��3��9�����ɵ�ֱ��MN�Ľ���ʽΪy=3x����P��PG��MN��y����G����ֱ��PG�Ľ���ʽΪy=3x-12��
ȡOG���е�F��0��-6����H��0��6��������F��MN��ƽ���߽���������E1��E2����ʱ��EMN�����=$\frac{1}{2}$��PMN�������ֱ��EF����ʽΪy=3x-6����$\left\{\begin{array}{l}{y=3x-6}\\{y=\frac{1}{2}��x-3��^{2}+3}\end{array}\right.$�ⷽ����ɵõ�E1��E2�������꣬ͬ���ɵ�E3��E4�����꣮
��� �⣺��1������ֱ��MN�Ľ���ʽΪy=kx+b��
��M��1��5����N��7��11�����������õ�$\left\{\begin{array}{l}{k+b=5}\\{7k+b=11}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=1}\\{b=4}\end{array}\right.$��
��ֱ��MN�Ľ���ʽΪy=x+4��
�ʴ�Ϊy=x+4��
��ֱ��x=3ƽ�֡�MPN��
��㣨6��$\frac{15}{2}$������ֱ��x=3�ĶԳƵ����������ϣ�
����0��$\frac{15}{2}$�����������ϣ�ֱ��AP�����㣨0��$\frac{15}{2}$����
��ֱ��PM�Ľ���ʽΪy=-$\frac{17}{6}$x+$\frac{15}{2}$��
��$\left\{\begin{array}{l}{y=-\frac{17}{6}x+\frac{15}{2}}\\{y=\frac{1}{2}��x-3��^{2}+3}\end{array}\right.$���$\left\{\begin{array}{l}{x=0}\\{y=\frac{15}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{59}{9}}\end{array}\right.$��
��M��$\frac{1}{3}$��$\frac{59}{9}$����N��6��$\frac{15}{2}$����
��ֱ��MN�Ľ���ʽΪy=$\frac{1}{6}$x+$\frac{13}{2}$��
�ʴ�Ϊy=$\frac{1}{6}$x+$\frac{13}{2}$��
�ڲ���Q��3��6-t�����������£�
֤������ֱ��MN�Ľ���ʽ��y=kx+b����k��0����
��$\left\{\begin{array}{l}{y=kx+b}\\{y=\frac{1}{2}��x-3��^{2}+3}\end{array}\right.$��x2-��2k+6��x+15-2b=0
��xM+xN=2k+6��xM•xN=15-2b��
��tan��MPQ=tan��NPQ����
$\frac{3-{x}_{M}}{{y}_{M}-t}$=$\frac{{x}_{N}-3}{{y}_{N}-t}$�������12k-2kb-2kt-6k2=0��
��k��0
��6-b-t-3k=0��
��b=6-t-3k��
��y=kx+6-t-3k=k��x-3��+6-t��
��Q��3��6-t����
�ʴ�Ϊ��3��6-t����
��2����ͼ2�У�
�����⣬Q��3��9����ֱ��MN������0��0����Q��3��9����
��ֱ��MN�Ľ���ʽΪy=3x��
��P��PG��MN��y����G����ֱ��PG�Ľ���ʽΪy=3x-12��
ȡOG���е�F��0��-6����H��0��6����
����F��MN��ƽ���߽���������E1��E2����ʱ��EMN�����=$\frac{1}{2}$��PMN�������
ֱ��EF����ʽΪy=3x-6��
��$\left\{\begin{array}{l}{y=3x-6}\\{y=\frac{1}{2}��x-3��^{2}+3}\end{array}\right.$���$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$��$\left\{\begin{array}{l}{x=9}\\{y=21}\end{array}\right.$��
��E1��9��21����E2��3��3����
����H��MN��ƽ���ߣ��������߽��ڵ�E3��E4����ʱ��ʱ��EMN�����=$\frac{1}{2}$��PMN�������
ֱ��EH�Ľ���ʽΪy=3x+6��
��$\left\{\begin{array}{l}{y=3x+6}\\{y=\frac{1}{2}��x-3��^{2}+3}\end{array}\right.$���$\left\{\begin{array}{l}{x=6-\sqrt{33}}\\{y=24-3\sqrt{33}}\end{array}\right.$��$\left\{\begin{array}{l}{x=6+\sqrt{33}}\\{y=24+3\sqrt{33}}\end{array}\right.$��
��E3��6+$\sqrt{33}$��24+3$\sqrt{33}$����E4��6-$\sqrt{33}$��24-3$\sqrt{33}$����
�������������������ĵ�E������Ϊ��9��21����3��3����6+$\sqrt{33}$��24+3$\sqrt{33}$����6-$\sqrt{33}$��24-3$\sqrt{33}$����
���� ���⿼����κ����ۺ��⡢һ�κ�����Ӧ�á�ֱ�߹��������⡢�����ε�������⡢��ֱ��ƽ�е�������֪ʶ������Ĺؼ���ѧ�����öԳƽ�����⣬���������ѧ֪ʶ��ѧ������ƽ���߽��������⣬������ת��Ϊ�ⷽ���������꣬�����п�ѹ���⣮


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 28�� | B�� | 68�� | C�� | 118�� | D�� | 90�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ABC��
��ͼ����֪��ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
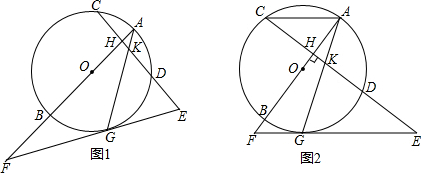
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{3}$ | B�� | $\frac{1}{3}$ | C�� | -3 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��У����һ�ǣ��е�ͬѧΪ��ʡʱ��ͼ���㣬�ڻ����вȳ���һ��С������Щͬѧ����������ѧ�����ǣ�������
��ͼ��У����һ�ǣ��е�ͬѧΪ��ʡʱ��ͼ���㣬�ڻ����вȳ���һ��С������Щͬѧ����������ѧ�����ǣ�������| A�� | �㶯���� | B�� | ����֮��ֱ����� | ||
| C�� | ����֮���߶���� | D�� | ����ȷ��һ��ֱ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ȱ������� | B�� | ������� | C�� | ƽ���ı��� | D�� | �������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com