
����Ŀ�������꼶��ʦ���Ծ���������ѧ�������������Ƚ������۵��飬��������ĿΪ�������ɡ�����˼����רע������������Ŀ��������������ȡ������������ѧ���IJ�����������Ƴ���ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ�������������������ͼ��������Ϣ����������⣺ 
��1������������У�һ���������ѧ����
��2��������ͳ��ͼ�У���Ŀ���������ɡ����ڵ����ε�Բ�ĽǵĶ���Ϊ�ȣ�
��3���뽫Ƶ���ֲ�ֱ��ͼ����������
��4�����ȫ����6000������ѧ������ô���Ծ��������У�������˼�����ij���ѧ��Լ�ж����ˣ�
���𰸡�
��1��560
��2��54
��3���⣺��������Ŀ���������ǣ�560��84��168��224=84���ˣ���
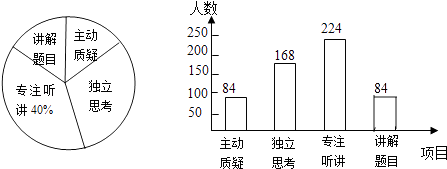 ��
��
��4���⣺���Ծ��������У�������˼�����ij���ѧ��Լ�У�6000�� ![]() =1800���ˣ���
=1800���ˣ���
���������⣺��1��������������ǣ�224��40%=560���ˣ����ʴ��ǣ�560����2�����������ɡ����ڵ����ε�Բ�ĽǵĶ����ǣ�360�� ![]() =54�㣬�ʴ��ǣ�54�� ��1������רע������������224�ˣ���ռ�ı�����40%��������ó�������������2������360���Զ�Ӧ�İٷֱȼ�����⣻��3��������������ȥ���������������������ý�����Ŀ���������Ӷ�����Ƶ���ֲ�ֱ��ͼ����4������6000���Զ�Ӧ�ı������ɣ�
=54�㣬�ʴ��ǣ�54�� ��1������רע������������224�ˣ���ռ�ı�����40%��������ó�������������2������360���Զ�Ӧ�İٷֱȼ�����⣻��3��������������ȥ���������������������ý�����Ŀ���������Ӷ�����Ƶ���ֲ�ֱ��ͼ����4������6000���Զ�Ӧ�ı������ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AC=BD=6��E��F��G��H�ֱ���AB��BC��CD��DA���е㣬��EG2+FH2= �� 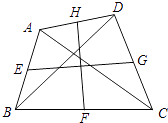
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������������������С������ĵڶ��꣬Ϊ�˸��õ����á������������С��������н�������ز��Ŷ�ij��ѧѧ�������ġ���֪���ʣ���ȡ��������ķ��������ʾ����飬��������Ϊ���dz��˽⡱������У�˽⡱���������˽⡱���͡����˽⡱�ĸ��ȼ���С�Ը��ݵ�������������ͼ��ʾ��ͳ��ͼ��������ṩ����Ϣ�ش����⣺ 
��1�����ε����У�������������
��2������ͳ��ͼ�С������˽⡱��������Ӧ��Բ�ĽǵĶ��������ڸ�У2000��ѧ�����������һ��ѧ�����ԡ����ġ����˽�ĸ��ʹ���ֵΪ��
��3���벹ȫƵ���ֲ�ֱ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱߡ�ABC�У���D��E�ֱ��ڱ�BC��AC�ϣ���BD=CE��AD��BE�ཻ�ڵ�F�� 
��1����֤��AD=BE��
��2�����AFE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������Լ��ɽ���ס������˾����ĸ߶�y���ף����ɽʱ��x���֣�֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ������˵����ȷ�ĸ���Ϊ�� �� ��1 ����ɽ�������ٶ���ÿ����10�ף���2������A��ʱ�����ĸ߶�bΪ30�ף���3���������ٺ��ҵĵ�ɽ�����ٶ��Ǽ�ɽ�����ٶȵ�3�����ҵ�ɽ1����ʱ�������ĸ߶�Ϊ15�ף���4����ɽʱ��Ϊ4���ӣ�9���ӣ�15����ʱ���ס������˾����ĸ߶Ȳ�Ϊ50�ף�
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�����װ����������������������dz���ɫ�ⶼ��ͬ�������������һ������ɫ��Żش��У����ҡ�Ⱥ����������һ�����ζ���������ĸ����ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ABΪֱ���ġ�O�ֱ�AC��BC�ڵ�D��E������ED����ED=EC��
��1����֤��AB=AC��
��2����գ�����AB=6��CD=4����BC=��
������OD������A�Ķ���Ϊʱ���ı���ODEB�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=x2+ ![]() ��y���ཻ�ڵ�A����B���O���ڵ�A�Գ�
��y���ཻ�ڵ�A����B���O���ڵ�A�Գ�
��1����գ���B����������
��2������B��ֱ��y=kx+b������k��0����x���ཻ�ڵ�C������C��ֱ��lƽ����y�ᣬP��ֱ��l��һ�㣬��PB=PC�����߶�PB�ij����ú�k��ʽ�ӱ�ʾ�������жϵ�P�Ƿ����������ϣ�˵�����ɣ�
��3���ڣ�2���������£�����C����ֱ��BP�ĶԳƵ�C��ǡ�����ڸ������ߵĶԳ����ϣ����ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
�Ͽ�ʱ����ʦ�������һ�����⣺��������ʵ��x������x�IJ���ʽx2��2x��1��a��0���������a��ȡֵ��Χ��
С�ݵ�˼·�ǣ�ԭ����ʽ�ȼ���x2��2x��1��a���躯��y1=x2��2x��1��y2=a����������������ͼ���ʾ��ͼ������ԭ����ת��Ϊ����y1��ͼ����y2��ͼ���Ϸ�ʱa��ȡֵ��Χ��
��1������С�ݵ�˼·�ش�
��������ʵ��x������x�IJ���ʽx2��2x��1��a��0���������a��ȡֵ��Χ�� ��
��2���ο�С��˼������ķ�����������⣺
����x�ķ���x��4= ![]() ��0��a��4��Χ���������⣬��a��ȡֵ��Χ��
��0��a��4��Χ���������⣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com