
【题目】如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2= . 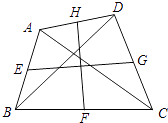
【答案】36
【解析】解:如右图,连接EF,FG,GH,EH, ∵E、H分别是AB、DA的中点,
∴EH是△ABD的中位线,
∴EH= ![]() BD=3,
BD=3,
同理可得EF,FG,GH分别是△ABC,△BCD,△ACD的中位线,
∴EF=GH= ![]() AC=3,FG=
AC=3,FG= ![]() BD=3,
BD=3,
∴EH=EF=GH=FG=3,
∴四边形EFGH为菱形,
∴EG⊥HF,且垂足为O,
∴EG=2OE,FH=2OH,
在Rt△OEH中,根据勾股定理得:OE2+OH2=EH2=9,
等式两边同时乘以4得:4OE2+4OH2=9×4=36,
∴(2OE)2+(2OH)2=36,
即EG2+FH2=36.
所以答案是:36.
【考点精析】通过灵活运用勾股定理的概念和三角形中位线定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半即可以解答此题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0.
(1)试判断原方程根的情况;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1 , 0),B(x2 , 0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.(友情提示:AB=|x2﹣x1|)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用四条线段首尾相接连成一个框架,其中AB=12,BC=14,CD=18,DA=24,则A、B、C、D任意两点之间的最长距离为( ) 
A.24cm
B.26cm
C.32cm
D.36cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y=﹣2x与二次函数y=ax2+2ax+c的图象交于A、B两点(点A在点B的右侧),与其对称轴交于点C.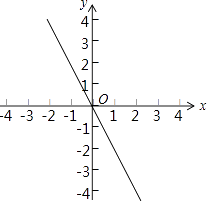
(1)求点C的坐标;
(2)设二次函数图象的顶点为D,点C与点D关于x轴对称,且△ACD的面积等于2.
①求二次函数的解析式;
②在该二次函数图象的对称轴上求一点P(写出其坐标),使△PBC与△ACD相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲乙两公司合作,12天可以完成,如果甲乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,求甲乙两公司单独完成这项工程,各需多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+4x的顶点为A,与x轴分别交于O、B两点,过顶点A分别作AC⊥x轴于点C,AD⊥y轴于点D,连接BD,交AC于点E,则△ADE与△BCE的面积和为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( ) 
A.55°
B.65°
C.75°
D.85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题: 
(1)在这次评价中,一共抽查了名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com