
【题目】已知:如图,一次函数y=﹣2x与二次函数y=ax2+2ax+c的图象交于A、B两点(点A在点B的右侧),与其对称轴交于点C.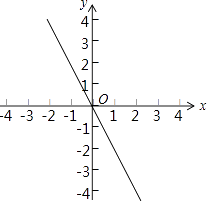
(1)求点C的坐标;
(2)设二次函数图象的顶点为D,点C与点D关于x轴对称,且△ACD的面积等于2.
①求二次函数的解析式;
②在该二次函数图象的对称轴上求一点P(写出其坐标),使△PBC与△ACD相似.
【答案】
(1)
解:∵y=ax2+2ax+c=a(x+1)2+c﹣a,
∴它的对称轴为x=﹣1.
又∵一次函数y=﹣2x与对称轴交于点C,
∴y=2.
∴C点的坐标为(﹣1,2)
(2)
解:①∵点C与点D 关于x轴对称,
∴点D的坐标为(﹣1,﹣2).
∴CD=4,
∵△ACD的面积等于2.
∴点A到CD的距离为1,C点与原点重合,点A的坐标为(0,0).
设二次函数为y=a(x+1)2﹣2过点A,则a=2,
∴y=2x2+4x.
②设P(﹣1,t).
交点B的坐标为(﹣3,6),D(﹣1,﹣2),C(﹣1,2),A(0,0),
则BC=2 ![]() ,PC=t﹣2,CD=4,AD=
,PC=t﹣2,CD=4,AD= ![]() ,
,
①当△PBC∽△CAD时, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t=10,
故点P的坐标为(﹣1,10),
②当△PBC∽△ACD时, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t= ![]() ,
,
故点P的坐标为(﹣1, ![]() ),
),
综上所述,点P的坐标为(﹣1,10),(﹣1, ![]() ).
).
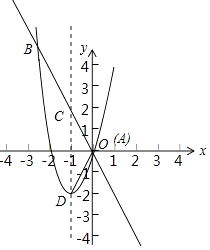
【解析】(1)把抛物线对称轴方程x=﹣1代入直线方程,求得相应的纵坐标,易得点C的坐标;(2)①根据点的坐标的对称性易得抛物线顶点坐标D(﹣1,﹣2),故CD=4,结合三角形的面积公式可以求得点A的坐标,将点A的坐标分别代入抛物线解析式为y=a(x+1)2﹣2,利用待定系数法求得抛物线的解析式即可;②需要分类讨论:△PBD∽△CAD、△PBD∽△ACD.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②![]() >0;③ac﹣b+1=0;④OAOB=﹣
>0;③ac﹣b+1=0;④OAOB=﹣![]() .
.
其中正确结论的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y= ![]() (x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为 .
(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+6分别与x轴、y轴交于A、B两点,直线y=
x+6分别与x轴、y轴交于A、B两点,直线y= ![]() x与AB交于点C,与过点A且平行于y轴的直线交于点D,点E从点A出发,以每秒1个单位的速度沿x轴向左运动,过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为ts(t>0).
x与AB交于点C,与过点A且平行于y轴的直线交于点D,点E从点A出发,以每秒1个单位的速度沿x轴向左运动,过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为ts(t>0).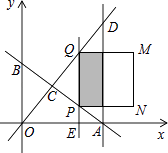
(1)求点C的坐标;
(2)当0<t<5时,求S的最大值;
(3)当t在何范围时,点(4, ![]() )被正方形PQMN覆盖?请直接写出t的取值范围.
)被正方形PQMN覆盖?请直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G. 
(1)试说明DF=CE;
(2)若AC=BF=DF,求∠ACE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动,快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中AB所示;慢车离乙地的路程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段OC所示,根据图象进行以下研究.
解读信息:
(1)甲,乙两地之间的距离为 km;
(2)线段AB的解析式为;线段OC的解析式为;
(3)设快,慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台举办的“中国汉字听写大会”节目受到中学生的广泛关注,某中学为了了解学生对观看“中国汉字听写大会”节目的喜爱程度,对该校部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图.在条形图中,从左向右依次为A类(非常喜欢),B类(较喜欢),C类(一般),D类(不喜欢),请结合两幅统计图,回答下列问题
(1)写出本次抽样调查的样本容量;
(2)请补全两幅统计图;
(3)若该校有2000名学生.请你估计观看“中国汉字听写大会”节目不喜欢的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息,下列说法正确的个数为( ) (1 )甲登山上升的速度是每分钟10米;(2)乙在A地时距地面的高度b为30米;(3)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,乙登山1分钟时,距地面的高度为15米;(4)登山时间为4分钟,9分钟,15分钟时,甲、乙两人距地面的高度差为50米.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com