
【题目】如图,直线y=﹣ ![]() x+6分别与x轴、y轴交于A、B两点,直线y=
x+6分别与x轴、y轴交于A、B两点,直线y= ![]() x与AB交于点C,与过点A且平行于y轴的直线交于点D,点E从点A出发,以每秒1个单位的速度沿x轴向左运动,过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为ts(t>0).
x与AB交于点C,与过点A且平行于y轴的直线交于点D,点E从点A出发,以每秒1个单位的速度沿x轴向左运动,过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为ts(t>0).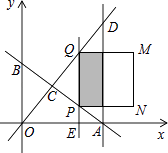
(1)求点C的坐标;
(2)当0<t<5时,求S的最大值;
(3)当t在何范围时,点(4, ![]() )被正方形PQMN覆盖?请直接写出t的取值范围.
)被正方形PQMN覆盖?请直接写出t的取值范围.
【答案】
(1)
解:由题意,得 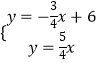 ,
,
解得: 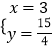 ,
,
∴C(3, ![]() )
)
(2)
解:∵直线y=﹣ ![]() x+6分别与x轴、y轴交于A、B两点,
x+6分别与x轴、y轴交于A、B两点,
∴y=0时,0=﹣ ![]() x+6,解得;x=8,
x+6,解得;x=8,
∴A点坐标为;(8,0),
根据题意,得AE=t,OE=8﹣t.
∴点Q的纵坐标为 ![]() (8﹣t),点P的纵坐标为﹣
(8﹣t),点P的纵坐标为﹣ ![]() (8﹣t)+6=
(8﹣t)+6= ![]() t,
t,
∴PQ= ![]() (8﹣t)﹣
(8﹣t)﹣ ![]() t=10﹣2t.
t=10﹣2t.
当MN在AD上时,10﹣2t=t,
∴t= ![]() .
.
当0<t≤ ![]() 时,S=t(10﹣2t),即S=﹣2t2+10t=﹣2(t﹣
时,S=t(10﹣2t),即S=﹣2t2+10t=﹣2(t﹣ ![]() )2+
)2+ ![]() ,S有最大值为
,S有最大值为 ![]() .
.
当 ![]() <t<5时,S=(10﹣2t)2,即S=4t2﹣40t+100=4(t﹣5)2,
<t<5时,S=(10﹣2t)2,即S=4t2﹣40t+100=4(t﹣5)2,
∵t<5时,S随t的增大而减小,
∴t= ![]() 时,S最大值=
时,S最大值= ![]() ,
,
∵ ![]() >
> ![]() ,
,
∴S的最大值为 ![]()
(3)
解:当t=5时,PQ=0,P,Q,C三点重合;
当t<5时,知OE=4时是临界条件,即8﹣t=4
即t=4
∴点Q的纵坐标为5> ![]() ,
,
点(4, ![]() )在正方形边界PQ上,E继续往左移动,则点(4,
)在正方形边界PQ上,E继续往左移动,则点(4, ![]() )进入正方形内部,但点Q的纵坐标再减少,当Q点的纵坐标为
)进入正方形内部,但点Q的纵坐标再减少,当Q点的纵坐标为 ![]() 时,OE=
时,OE= ![]() ,
,
∴8﹣t= ![]() ,解得:t=
,解得:t= ![]() ,
,
此时OE+PN= ![]() +PQ=
+PQ= ![]() +(10﹣2t)=
+(10﹣2t)= ![]() >4满足条件,
>4满足条件,
∴4<t< ![]() ,
,
当t>5时,由图和条件知,则有E(t﹣8,0),PQ=2t﹣10要满足点(4, ![]() )在正方形的内部,
)在正方形的内部,
则临界条件N点横坐标为44=PQ+OE=|2t﹣10|+|t﹣8|=3t﹣18
即t=6,此时Q点的纵坐标为:﹣ ![]() ×2+6=
×2+6= ![]() >
> ![]() .满足条件,
.满足条件,
∴t>6.
综上所述:4≤t≤ ![]() 或t≥6时,点(4,
或t≥6时,点(4, ![]() )被正方形PQMN覆盖.
)被正方形PQMN覆盖.
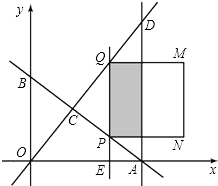
【解析】(1)简单求两直线的交点,得点C的坐标;(2)求得S与t之间的函数关系式;配方,即可求得二次函数的最大值,即可得出S的最大值;(3)求出定点在正方形PQMN内部时,t的范围,即可得出点(4, ![]() )被正方形PQMN覆盖时t的取值范围.要用到分类讨论.
)被正方形PQMN覆盖时t的取值范围.要用到分类讨论.
【考点精析】本题主要考查了二次函数的最值的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用四条线段首尾相接连成一个框架,其中AB=12,BC=14,CD=18,DA=24,则A、B、C、D任意两点之间的最长距离为( ) 
A.24cm
B.26cm
C.32cm
D.36cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某艺术工作室装配240件展品,这些展品分为A、B、C三种型号,它们的数量比例以及每人每小时组装各种型号展品的数量如图所示,若每人组装同一型号展品的速度相同,请根据以上信息,完成下列问题. 
(1)A型展品有件;B型展品有件;
(2)若每人组装A型展品16件,与组装C型展品12件所用的时间相同,求条形图中a的值及每人每小时组装C型展品的件数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y=﹣2x与二次函数y=ax2+2ax+c的图象交于A、B两点(点A在点B的右侧),与其对称轴交于点C.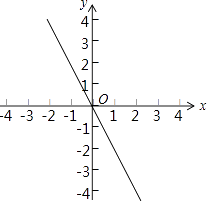
(1)求点C的坐标;
(2)设二次函数图象的顶点为D,点C与点D关于x轴对称,且△ACD的面积等于2.
①求二次函数的解析式;
②在该二次函数图象的对称轴上求一点P(写出其坐标),使△PBC与△ACD相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+4x的顶点为A,与x轴分别交于O、B两点,过顶点A分别作AC⊥x轴于点C,AD⊥y轴于点D,连接BD,交AC于点E,则△ADE与△BCE的面积和为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+ax+b的图象与y轴交于点A(0,﹣2),与x轴交于点B(1,0)和点C,D(m,0)(m>2)是x轴上一点.
(1)求二次函数的解析式;
(2)点E是第四象限内的一点,若以点D为直角顶点的Rt△CDE与以A,O,B为顶点的三角形相似,求点E坐标(用含m的代数式表示);
(3)在(2)的条件下,抛物线上是否存在一点F,使得四边形BCEF为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com