
【题目】根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①条边成比例的两个凸四边形相似;( 命题)
②三个角分别相等的两个凸四边形相似;( 命题)
③两个大小不同的正方形相似.( 命题)
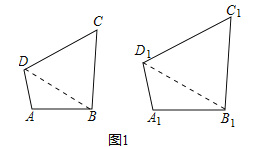
(2)如图1,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,![]() ,求证:四边形ABCD与四边形A1B1C1D1相似.
,求证:四边形ABCD与四边形A1B1C1D1相似.
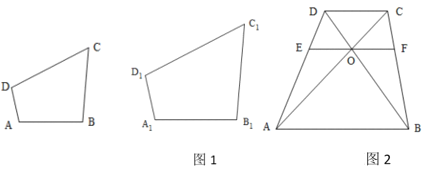
(3)如图2,四边形ABCD中,AB∥CD,AC与BD相交于点O,过点O作EF∥AB分别交AD,BC于点E,F.记四边形ABFE的面积为S1,四边形EFDE的面积为S2,若四边形ABFE与四边形EFCD相似,求![]() 的值.
的值.
【答案】(1)①假,②假,③真;(2)见解析 ;(3)![]()
【解析】
(1)根据相似多边形的定义即可判断.
(2)根据相似多边形的定义证明四边成比例,四个角相等即可.
(3)四边形ABFE与四边形EFCD相似,证明相似比是1即可解决问题,即证明DE=AE即可.
解(1)①四条边成比例的两个凸四边形相似,是假命题,角不一定相等.
②三个角分别相等的两个凸四边形相似,是假命题,边不一定成比例.
③两个大小不同的正方形相似.是真命题.
故答案为假,假,真.
(2)证明:分别连接BD,B1D1
![]() ,且
,且![]()
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 四边形ABCD与四边形A1B1C1D1相似.
四边形ABCD与四边形A1B1C1D1相似.
(3)如图2中,
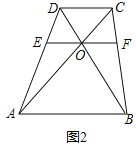
∵四边形ABFG与四边形EFCD相似
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即AE=DE
,即AE=DE
![]() ,
,


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料,按要求解答问题:
阅读理解:若p、q、m为整数,且三次方程![]() 有整数解c,则将c代入方程得:
有整数解c,则将c代入方程得:![]() ,移项得:
,移项得:![]() ,即有:
,即有:![]() ,由于
,由于![]() 与c及m都是整数,所以c是m的因数.
与c及m都是整数,所以c是m的因数.
上述过程说明:整数系数方程![]() 的整数解只可能是m的因数.
的整数解只可能是m的因数.
例如:方程![]() 中-2的因数为±1和±2,将它们分别代入方程
中-2的因数为±1和±2,将它们分别代入方程![]() 进行验证得:x=-2是该方程的整数解,-1、1、2不是方程的整数解.
进行验证得:x=-2是该方程的整数解,-1、1、2不是方程的整数解.
解决问题:
①根据上面的学习,请你确定方程![]() 的整数解只可能是哪几个整数?
的整数解只可能是哪几个整数?
②方程![]() 是否有整数解?若有,请求出其整数解;若没有,请说明理由.
是否有整数解?若有,请求出其整数解;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
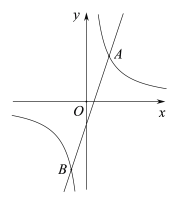
【题目】如图,反比例函数![]() 和一次函数y=kx-1的图象相交于A(m,2m),B两点.
和一次函数y=kx-1的图象相交于A(m,2m),B两点.
(1)求一次函数的表达式;
(2)求出点B的坐标,并根据图象直接写出满足不等式![]() 的x的取值范围.
的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市举办的以“校园文明”为主题的中小学生手抄报比赛中,各学校认真组织初赛并按比例筛选出较好的作品参加全市决赛,所有参加市级决赛的作品均获奖,奖项分为一等奖.二等奖、三等奖和优秀奖.现从参加决赛的作品中随机抽取部分作品并将获奖结果绘制成如下两幅统计图请你根据图中所给信息解答下列问题:

(1)一等奖所占的百分比是多少?三等奖的人数是多少?
(2)求三等奖所对应的扇形圆心角的度数;
(3)若参加决赛的作品有3000份,估计获得一等奖和二等奖的总人数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )

A.![]() n mileB.60 n mileC.120 n mileD.
n mileB.60 n mileC.120 n mileD.![]() n mile
n mile
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地间的直线公路长为![]() 千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发
千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发![]() 小时,途中轿车出现了故障,停下维修,货车仍继续行驶.
小时,途中轿车出现了故障,停下维修,货车仍继续行驶.![]() 小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离
小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离![]() (千米)与轿车所用的时间
(千米)与轿车所用的时间![]() (小时)的关系如图所示,请结合图象解答下列问题:
(小时)的关系如图所示,请结合图象解答下列问题:
(1)货车的速度是_______千米/小时;轿车的速度是_______千米/小时;![]() 值为_______.
值为_______.
(2)求轿车距其出发地的距离![]() (千米)与所用时间
(千米)与所用时间![]() (小时)之间的函数关系式并写出自变量
(小时)之间的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
(3)请直接写出货车出发多长时间两车相距![]() 千米.
千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
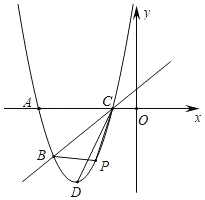
【题目】如图,已知抛物线y=ax2+bx+5经过A(﹣5,0),B(﹣4,﹣3)两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求△PBC的面积的最大值;
②该抛物线上是否存在点P,使得∠PBC=∠BCD?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题背景:
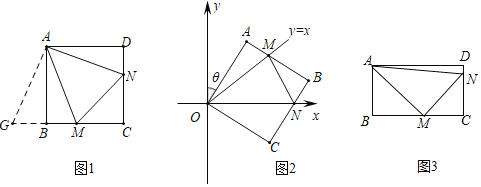
如图1,在正方形ABCD中,点M,N分别在边BC,CD上,连接MN,且∠MAN=45°,将△ADN绕点A顺时针旋转90°,得到△ABG,可证△AMG≌△AMN,易得线段MN、BM、DN之间的数量关系为: (直接填写);
(2)实践应用:
在平面直角坐标系中,边长为5的正方形OABC的两顶点分别在y轴、x轴的正半轴上,O在原点.现将正方形OABC绕点O按顺时针方向旋转,旋转角为θ,当点A第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.如图2,设△MBN的周长为P,在旋转正方形OABC的过程中,P值是否有变化?请证明你的结论;
(3)拓展研究:
如图3,将正方形改为长与宽不相等的矩形,且∠MAN=∠CMN=45°,请你直接写出线段MN、BM、DN之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
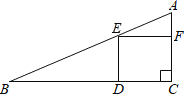
【题目】如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A. 100cm2B. 150cm2C. 170cm2D. 200cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com