
【题目】在某市举办的以“校园文明”为主题的中小学生手抄报比赛中,各学校认真组织初赛并按比例筛选出较好的作品参加全市决赛,所有参加市级决赛的作品均获奖,奖项分为一等奖.二等奖、三等奖和优秀奖.现从参加决赛的作品中随机抽取部分作品并将获奖结果绘制成如下两幅统计图请你根据图中所给信息解答下列问题:

(1)一等奖所占的百分比是多少?三等奖的人数是多少?
(2)求三等奖所对应的扇形圆心角的度数;
(3)若参加决赛的作品有3000份,估计获得一等奖和二等奖的总人数有多少?
【答案】(1)32人;(2)115.2°;(3)840人.
【解析】
(1)先求出抽样人数=优秀人数÷优秀百分比,用一等奖的人数除以总人数即可,三等奖百分比=1-(二等奖百分比+一等奖百分比+优秀奖百分比),再用三等奖百分比×总人数即可;(2)根据圆心角=360°×百分比计算即可;(3)一等奖和二等奖总人数=总份数×(一等奖百分比+优秀奖百分比)即可.
解:(1)由图可得:抽样人数为:40÷40%=100人,
∴一等奖所占的百分比是:8÷100×100%=8%
二等奖的人数为:100×20%=20人
∴三等奖的人数为:100﹣8﹣20﹣40=32人;
(2)三等奖所对应的扇形圆心角的度数为:32÷100×360°=115.2°
(3)一等奖和二等奖的总人数为:3000×![]() =840人.
=840人.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】天水市某中学为了解学校艺术社团活动的开展情况,在全校范围内随机抽取了部分学生,在“舞蹈、乐器、声乐、戏曲、其它活动”项目中,围绕你最喜欢哪一项活动(每人只限一项)进行了问卷调查,并将调查结果绘制成如下两幅不完整的统计图.
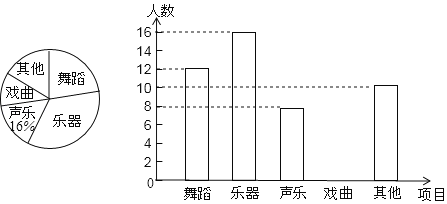
请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了 名学生.
(2)请你补全条形统计图.
(3)扇形统计图中喜欢“乐器”部分扇形的圆心角为 度.
(4)请根据样本数据,估计该校1200名学生中喜欢“舞蹈”项目的共多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国著名的数学家华罗庚曾巧解开立方的智力题:问题:59319是一个整数的立方,求这个整数?
解答:因为:10<![]() <100,所以:
<100,所以:![]() 是两位整数;
是两位整数;
因为:整数59319的末位上的数字是9,而整数0~9的立方中,只有93=729的末位数字是9,
所以:![]() 的末位数字是9;又因为划去59319的后面三位319得到59,而3<
的末位数字是9;又因为划去59319的后面三位319得到59,而3<![]() <4,
<4,
所以![]() 的十位数字是3;因此
的十位数字是3;因此![]() =39.
=39.
应用:已知2(2x﹣2)3+221184=0,其中x是整数.则x的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是BC边上的一个动点,沿着AE翻折矩形,使点B落在点F处若AB=3,BC=![]() AB,解答下列问题:
AB,解答下列问题:
(1)在点E从点B运动到点C的过程中,求点F运动的路径长;
(2)当点E是BC的中点时,试判断FC与AE的位置关系,并说明你的理由;
(3)当点F在矩形ABCD内部且DF=CD时,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①条边成比例的两个凸四边形相似;( 命题)
②三个角分别相等的两个凸四边形相似;( 命题)
③两个大小不同的正方形相似.( 命题)
(2)如图1,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,![]() ,求证:四边形ABCD与四边形A1B1C1D1相似.
,求证:四边形ABCD与四边形A1B1C1D1相似.
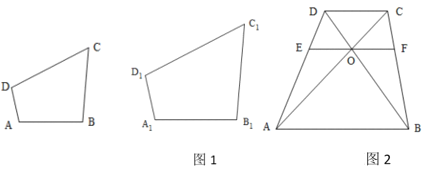
(3)如图2,四边形ABCD中,AB∥CD,AC与BD相交于点O,过点O作EF∥AB分别交AD,BC于点E,F.记四边形ABFE的面积为S1,四边形EFDE的面积为S2,若四边形ABFE与四边形EFCD相似,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2,且x1<1<x2,则c的取值范围是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
查看答案和解析>>
科目:初中数学 来源: 题型:
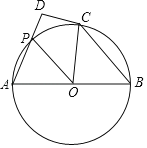
【题目】如图,已知AB是⊙O的直径,点P是⊙O上一点,连接OP,点A关于OP的对称点C恰好落在⊙O上.
(1)求证:OP∥BC;
(2)过点C作⊙O的切线CD,交AP的延长线于点D.如果∠D=90°,DP=1,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com