
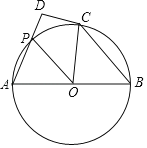
【题目】如图,已知AB是⊙O的直径,点P是⊙O上一点,连接OP,点A关于OP的对称点C恰好落在⊙O上.
(1)求证:OP∥BC;
(2)过点C作⊙O的切线CD,交AP的延长线于点D.如果∠D=90°,DP=1,求⊙O的直径.
【答案】(1)见解析;(2)⊙O的直径AB=4.
【解析】
(1)由题意可知![]() ,根据同弧所对的圆心角相等得到∠AOP=
,根据同弧所对的圆心角相等得到∠AOP=![]() ∠AOC,再根据同弧所对的圆心角和圆周角的关系得出∠ABC=
∠AOC,再根据同弧所对的圆心角和圆周角的关系得出∠ABC=![]() ∠AOC,利用同位角相等两直线平行,可得出PO与BC平行;
∠AOC,利用同位角相等两直线平行,可得出PO与BC平行;
(2)由CD为圆O的切线,利用切线的性质得到OC垂直于CD,又AD垂直于CD,利用平面内垂直于同一条直线的两直线平行得到OC与AD平行,根据两直线平行内错角相等得到∠APO=∠COP,由∠AOP=∠COP,等量代换可得出∠APO=∠AOP,再由OA=OP,利用等边对等角可得出一对角相等,等量代换可得出三角形AOP三内角相等,确定出三角形AOP为等边三角形,根据等边三角形的内角为60°得到∠AOP为60°,由OP平行于BC,利用两直线平行同位角相等可得出∠OBC=∠AOP=60°,再由OB=OC,得到三角形OBC为等边三角形,可得出∠COB为60°,利用平角的定义得到∠POC也为60°,再加上OP=OC,可得出三角形POC为等边三角形,得到内角∠OCP为60°,可求出∠PCD为30°,在直角三角形PCD中,利用30°所对的直角边等于斜边的一半可得出PD为PC的一半,而PC等于圆的半径OP等于直径AB的一半,可得出PD为AB的四分之一,即AB=4PD=4.
(1)证明:∵A关于OP的对称点C恰好落在⊙O上.
∴![]()
∴∠AOP=∠COP,
∴∠AOP=![]() ∠AOC,
∠AOC,
又∵∠ABC=![]() ∠AOC,
∠AOC,
∴∠AOP=∠ABC,
∴PO∥BC;
(2)解:连接PC,
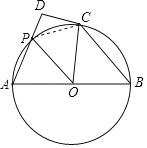
∵CD为圆O的切线,
∴OC⊥CD,又AD⊥CD,
∴OC∥AD,
∴∠APO=∠COP,
∵∠AOP=∠COP,
∴∠APO=∠AOP,
∴OA=AP,
∵OA=OP,
∴△APO为等边三角形,
∴∠AOP=60°,
又∵OP∥BC,
∴∠OBC=∠AOP=60°,又OC=OB,
∴△BCO为等边三角形,
∴∠COB=60°,
∴∠POC=180°﹣(∠AOP+∠COB)=60°,又OP=OC,
∴△POC也为等边三角形,
∴∠PCO=60°,PC=OP=OC,
又∵∠OCD=90°,
∴∠PCD=30°,
在Rt△PCD中,PD=![]() PC,
PC,
又∵PC=OP=![]() AB,
AB,
∴PD=![]() AB,
AB,
∴AB=4PD=4.


科目:初中数学 来源: 题型:
【题目】如图,圆心在坐标原点的⊙O,与坐标轴的交点分别为A、B和C、D.弦CM交OA于P,连结AM,已知tan∠PCO=![]() ,PC、PM是方程x2﹣px+20=0的两根.
,PC、PM是方程x2﹣px+20=0的两根.
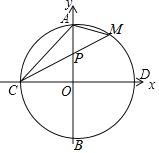
(1)求C点的坐标;
(2)写出直线CM的函数解析式;
(3)求△AMC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为 人,扇形统计图中,希望参加活动D所占圆心角为 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
.

(1)经过怎样的平移,可使△ABC的顶点A与坐标原点O重合,并直接写出此时点C 的对应点![]() 坐标;(不必画出平移后的三角形);
坐标;(不必画出平移后的三角形);
(2)将△ABC绕坐标原点![]() 逆时针旋转90°,得到△A′B′C′,画出△A′B′C′;
逆时针旋转90°,得到△A′B′C′,画出△A′B′C′;
(3)在(2)问的条件下,求线段BC扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
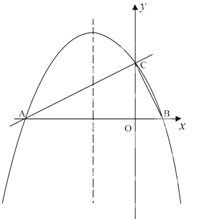
【题目】如图,在平面直角坐标系xoy中,直线![]() 与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是
与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
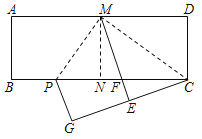
【题目】如图,在矩形ABCD中,AD=2![]() AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:
AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:
①△CMP是直角三角形;
②点C、E、G不在同一条直线上;
③PC=![]() MP;
MP;
④BP=![]() AB;
AB;
⑤PG=2EF.
其中一定成立的是_____(把所有正确结论的序号填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,过点B有一条直线1与正方形ABCD的对角线AC所在直线相交于点G,过点C、A分别作直线1的垂线段CE、AF于点E、F,对角线AC、BD相交于点O,连接OE、OF.
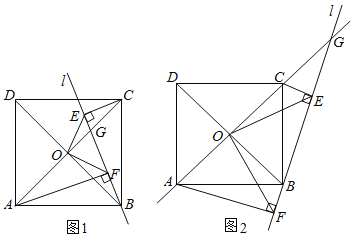
(1)如图1,猜测OE、OF有怎样的数量关系和位置关系,并说明理由;
(2)若正方形边长为10.
①若直线1在如图1的位置,当![]() 时,求EG的长;
时,求EG的长;
②若直线1在如图2的位置,当![]() 时,请直接写出EG的长.
时,请直接写出EG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com