
【题目】如图,在矩形ABCD中,AD=2![]() AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:
AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:
①△CMP是直角三角形;
②点C、E、G不在同一条直线上;
③PC=![]() MP;
MP;
④BP=![]() AB;
AB;
⑤PG=2EF.
其中一定成立的是_____(把所有正确结论的序号填在横线上).
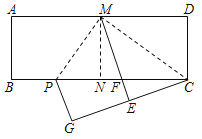
【答案】①④⑤
【解析】
由折叠的性质,可得∠DMC=∠EMC,CD=CE,∠AMP=∠EMP,AB=GE,由平角的定义可求∠PME+∠CME=![]() ×180°=90°,可判断①正确;由折叠的性质可得∠GEC=180°,可判断②正确;设AB=x,则AD=2
×180°=90°,可判断①正确;由折叠的性质可得∠GEC=180°,可判断②正确;设AB=x,则AD=2![]() x,由勾股定理可求MP和PC的长,即可判断③错误,先求出PB=
x,由勾股定理可求MP和PC的长,即可判断③错误,先求出PB=![]() x,即可判断④正确,由平行线分线段成比例可求PG=2EF,可判断⑤正确,即可求解.
x,即可判断④正确,由平行线分线段成比例可求PG=2EF,可判断⑤正确,即可求解.
∵沿着CM折叠,点D的对应点为E,
∴∠DMC=∠EMC,CD=CE,
∵再沿着MP折叠,使得AM与EM重合,折痕为MP,
∴∠AMP=∠EMP,AB=GE,
∵∠AMD=180°,
∴∠PME+∠CME=![]() ×180°=90°,
×180°=90°,
∴△CMP是直角三角形;故①正确;
∵沿着CM折叠,点D的对应点为E,
∴∠D=∠MEC=90°,
∵再沿着MP折叠,使得AM与EM重合,折痕为MP,
∴∠MEG=∠A=90°,
∴∠GEC=180°,
∴点C、E、G在同一条直线上,故②错误;
∵AD=2![]() AB,
AB,
∴设AB=x,则AD=2![]() x,
x,
∵将矩形ABCD对折,得到折痕MN;
∴DM=![]() AD=
AD=![]() x,
x,
∴CM=![]() x,
x,
∵∠PMC=90°,MN⊥PC,
∴CM2=CNCP,
∴CP=![]() x,
x,
∴PN=CP-CN=![]() x,
x,
∴PM=![]() x,
x,
∴![]() ,
,
∴PC=![]() PM,故③错误,
PM,故③错误,
∵PC=![]() x,
x,
∴PB=BC-PC=2![]() x-
x-![]() x=
x=![]() x,
x,
∴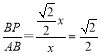 ,
,
∴BP=![]() AB,故④正确,
AB,故④正确,
∵∠MEC=∠G=90°,
∴PG∥ME,
∴![]() ,
,
∵AB=GE=CD=CE,
∴CG=2CE,
∴PG=2EF,故⑤正确,
故答案为:①④⑤.


科目:初中数学 来源: 题型:
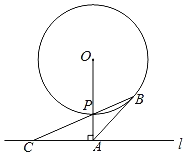
【题目】如图,直线l与⊙O相离,OA⊥![]() 于点A,与⊙O相交于点P,OA=5.C是直线
于点A,与⊙O相交于点P,OA=5.C是直线![]() 上一点,连结CP并延长交⊙O于另一点B,且AB=AC.
上一点,连结CP并延长交⊙O于另一点B,且AB=AC.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为3,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c和直线y=x+1交于A,B两点,点A在x轴上,点B在直线x=3上,直线x=3与x轴交于点C

(1)求抛物线的解析式;
(2)点P从点A出发,以每秒![]() 个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
①当t为何值时,矩形PQNM的面积最小?并求出最小面积;
②直接写出当t为何值时,恰好有矩形PQNM的顶点落在抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送花,感恩母亲,祝福母亲.今年节日前夕,某花店采购了一批康乃馨,经分析上一年的销售情况,发现这种康乃馨每天的销售量y(支)是销售单价x(元)的一次函数,已知销售单价为7元/支时,销售量为16支;销售单价为8元/支时,销售量为14支.
(1)求这种康乃馨每天的销售量y(支)关于销售单价x(元/支)的一次函数解析式;
(2)若按去年方式销售,已知今年这种康乃馨的进价是每支5元,商家若想每天获得42元的利润,销售单价要定为多少元?
(3)在(2)的条件下,当销售单价x为何值时,花店销售这种康乃馨每天获得的利润最大?并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
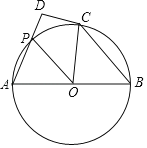
【题目】如图,已知AB是⊙O的直径,点P是⊙O上一点,连接OP,点A关于OP的对称点C恰好落在⊙O上.
(1)求证:OP∥BC;
(2)过点C作⊙O的切线CD,交AP的延长线于点D.如果∠D=90°,DP=1,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
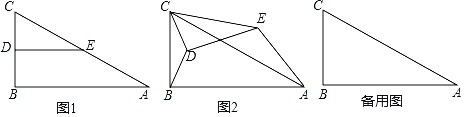
【题目】如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,![]() =_______;
=_______;
②当α=180°时,![]() =______.
=______.
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以边AB为直径的⊙O交边BC于点D,交边AC于点E.过D点作DF⊥AC于点F.
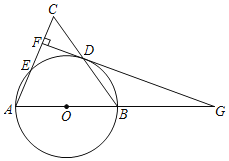
(1)求证:DF是⊙O的切线;
(2)求证:CF=EF;
(3)延长FD交边AB的延长线于点G,若EF=3,BG=9时,求⊙O的半径及CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com