
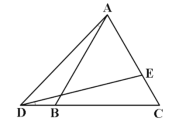
【题目】如图,等边三角形![]() 中,
中,![]() ,点D是
,点D是![]() 延长线上一点,且
延长线上一点,且![]() ,点E在直线
,点E在直线![]() 上,当
上,当![]() 时,
时,![]() 的长为_____.
的长为_____.
【答案】2或![]() .
.
【解析】
分①在线段AC上,②在线段AC的延长线上两种情况讨论.对于①作EF//AB与BC相交于F,证明△DFE∽△ABD,利用相似三角形对应边相等可求得EC,即也可求得AE;对于②作EF//AB与BC的延长线交于F,证明△DCE∽△ABD,利用相似三角形对应边相等可求得EC,即也可求得AE.
解:E点的位置有两种可能,①在线段AC上,②在线段AC的延长线上. E不可能在CA的延长线上(因为若E在CA的延长线上由①可知![]() 不可能等于
不可能等于![]() ).
).
①若E在线段AC上,如图作EF//AB与BC相交于F,

∵![]() 为等边三角形,
为等边三角形,![]() ,
,
∴AC=BC=AB=3,![]() ,
,
∴∠ABD=120°,
∵EF//AB,
∴![]() ,
,
∴△EFC为等边三角形,∠EFD=120°,设EF=FC=EC=x.
∵![]() ,∠ABD=∠EFD=120°,
,∠ABD=∠EFD=120°,
∴△DFE∽△ABD,
∴![]()
∵![]() ,
,
∴![]()
∴![]() ,解得
,解得![]()
∴EF=FC=EC=1,
∴AE=AC-EC=3-1=2;
②若E点在线段AC的延长线上,作EF//AB与BC的延长线交于F.
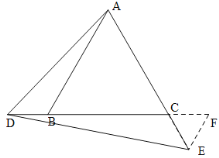
与①同理可证△EFC为等边三角形,∠ECD=120°,设EF=FC=EC=x.
∵![]() ,∠ABD=∠ECD=120°,
,∠ABD=∠ECD=120°,
∴△DCE∽△ABD,
∴![]() ,
,
∵![]() ,
,
∴BD=BC+BD=4,
∴![]() ,解得
,解得![]() ,
,
∴EF=FC=EC=![]() ,
,
![]() ,
,
故答案为:2或![]() .
.


科目:初中数学 来源: 题型:
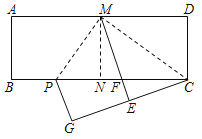
【题目】如图,在矩形ABCD中,AD=2![]() AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:
AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:
①△CMP是直角三角形;
②点C、E、G不在同一条直线上;
③PC=![]() MP;
MP;
④BP=![]() AB;
AB;
⑤PG=2EF.
其中一定成立的是_____(把所有正确结论的序号填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
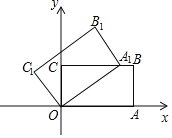
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明调查了本校九年级300名学生到校的方式,根据调査结果绘制出统计图的一部分如图:
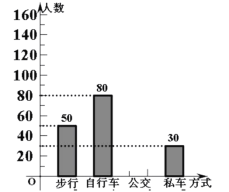
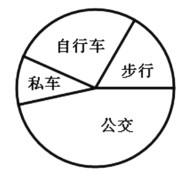
(1)补全条形统计图;
(2)求扇形统计图中表示“步行”的扇形圆心角的度数;
(3)请估计在全校1200名学生中乘公交的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
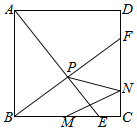
【题目】如图,正方形ABCD的边长为2,点E,点F分别是边BC,边CD上的动点,且BE=CF,AE与BF相交于点P.若点M为边BC的中点,点N为边CD上任意一点,则MN+PN的最小值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
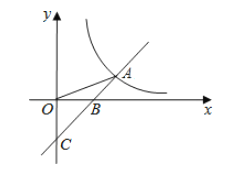
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,连接
,连接![]() ,且
,且![]() .则不等式
.则不等式![]() 的解集为( )
的解集为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.-3<x<0或x>3
D.-3<x<0或x>3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com