
【题目】如图,圆心在坐标原点的⊙O,与坐标轴的交点分别为A、B和C、D.弦CM交OA于P,连结AM,已知tan∠PCO=![]() ,PC、PM是方程x2﹣px+20=0的两根.
,PC、PM是方程x2﹣px+20=0的两根.
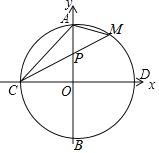
(1)求C点的坐标;
(2)写出直线CM的函数解析式;
(3)求△AMC的面积.
【答案】(1)点C坐标(﹣6,0);(2)y=![]() x+4;(3)△AMC的面积为
x+4;(3)△AMC的面积为![]() .
.
【解析】
(1)连接BC,根据一元二次方程根与系数的关系可求PCPM=20,然后根据锐角三角函数设CO=3x,PO=2x,利用x表示出AP和BP,然后证出△AMP∽△CBP,列出比例式即可求出结论;
(2)设直线CM的函数解析式为:y=kx+b,将点C、P的坐标代入即可求出结论;
(3)过点M作MN⊥AB于N,利用勾股定理求出PC即可求出PM,然后证出MN∥CO,即可证出△CPO∽△MPN,然后列出比例式即可求出MN,最后利用△AMC的面积=![]() ×AP×(CO+MN)即可求出结论.
×AP×(CO+MN)即可求出结论.
(1)如图,连接BC,

∵PC、PM是方程x2﹣px+20=0的两根.
∴PCPM=20,
∵tan∠PCO=![]() =
=![]() ,
,
∴设CO=3x,PO=2x,
∵圆心在坐标原点的⊙O,与坐标轴的交点分别为A、B和C、D,
∴OC=OB=OD=OA=3x,
∴AP=x,
∴BP=5x,
∵∠AMC=∠CBA,∠APM=∠BPC,
∴△AMP∽△CBP,
∴![]() ,
,
∴PCPM=APPB=20,
∴x5x=20,
∴x=2,x=-2(舍去)
∴CO=6,OP=4,
∴点C坐标(﹣6,0);
(2)∵OP=4,
∴点P(0,4)
设直线CM的函数解析式为:y=kx+b,
∴![]()
解得:![]()
∴直线CM的函数解析式为:y=![]() x+4,
x+4,
(3)如图,过点M作MN⊥AB于N,

∵CO=6,OP=4,
∴CP=![]() =
=![]() =2
=2![]() ,
,
∵CPPM=20,
∴PM=![]() ,
,
∵MN⊥AB,CO⊥AB,
∴MN∥CO,
∴△CPO∽△MPN,
∴![]() ,
,
∴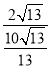 =
=![]()
∴MN=![]() ,
,
∵△AMC的面积=![]() ×AP×(CO+MN)=
×AP×(CO+MN)=![]() ×2×(6+
×2×(6+![]() )=
)=![]() .
.


科目:初中数学 来源: 题型:
【题目】某店因为经营不善欠下68400元的无息贷款的债务,想转行经营服装专卖店又缺少资金.“中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息).已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量![]() (件)与销售价
(件)与销售价![]() (元件)之间的关系可用图中的一条折线(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含债务).
(元件)之间的关系可用图中的一条折线(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含债务).
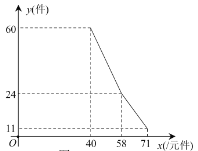
(1)求日销售量![]() (件)与销售价
(件)与销售价![]() (元/件)之间的函数关系式;
(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还债务,当某天的销售价为48元/件时,当天正好收支平衡(收入=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店最早需要多少天能还清所有债务,此时每件服装的价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
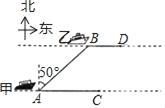
【题目】如图,海面上甲、乙两船分别从A,B两处同时出发,由西向东行驶,甲船的速度为24n mile/h,乙船的速度为15n mile/h,出发时,测得乙船在甲船北偏东50°方向,且AB=10nmile,经过20分钟后,甲、乙两船分别到达C,D两处.
(参考值:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
(1)求两条航线间的距离;
(2)若两船保持原来的速度和航向,还需要多少时间才能使两船的距离最短?(精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正六边形ABCDEF放置在直角坐标系内,A(﹣2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2020次翻转之后,点C的坐标是_____.
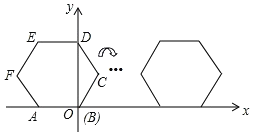
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒爆发,教育部部署了“停课不停学”的有关工作,各地都在进行在线教育.小依同学为了了解网课学习情况,对本班部分同学最喜爱的课程进行了调查,调查课程分别是网上授课、体育锻炼、名著阅读、艺术欣赏和其他课程并制成以下两幅不完整的统计图, 请你根据图中提供的信息解答下列问题:
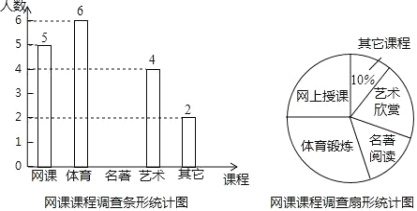
(1)求本次调查中一共调查了多少名学生,及其中“名著阅读”所占的圆心角度数 .
(2)请把条形统计图补全.
(3)若该校一共有 3000 名学生,请估算出全校最喜爱的课程是“体育锻炼”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O.AC=8cm,BD=6cm,点P为AC上一动点,点P以1cm/的速度从点A出发沿AC向点C运动.设运动时间为ts,当t=_____s时,△PAB为等腰三角形.
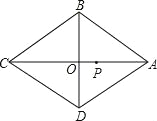
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进![]() 、
、![]() 两种粽子1100个,购买
两种粽子1100个,购买![]() 种粽子与购买
种粽子与购买![]() 种粽子的费用相同,已知
种粽子的费用相同,已知![]() 粽子的单价是
粽子的单价是![]() 种粽子单价的1.2倍.
种粽子单价的1.2倍.
(1)求![]() 、
、![]() 两种粽子的单价各是多少?
两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买![]() 、
、![]() 两种粽子共2600个,已知
两种粽子共2600个,已知![]() 、
、![]() 两种粽子的进价不变,求
两种粽子的进价不变,求![]() 中粽子最多能购进多少个?
中粽子最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
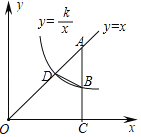
【题目】如图,直线y=x与反比例函数y=![]() (x>0)的图象相交于点D,点A为直线y=x上一点,过点A作AC⊥x轴于点C,交反比例函数y=
(x>0)的图象相交于点D,点A为直线y=x上一点,过点A作AC⊥x轴于点C,交反比例函数y=![]() (x>0)的图象于点B,连接BD.
(x>0)的图象于点B,连接BD.
(1)若点B的坐标为(8,2),则k= ,点D的坐标为 ;
(2)若AB=2BC,且△OAC的面积为18,求k的值及△ABD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com