Question

（本题满分10分）

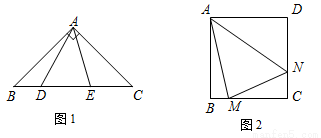
【操作探究】如图1，在Rt△ABC中，∠BAC=90°，AB=AC，点D，E是BC边上的任意两点，且∠DAE=45°．

（1）将△ABD绕点A逆时针旋转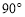，得到△ACF，请在图（1）中画出△ACF．

（2）在（1）中，连接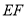，探究线段BD，EC和DE之间有怎样的数量关系？写出猜想，并说明理由．

【方法应用】

（3）如图2，M，N分别是正方形ABCD的边BC，CD上一点，且BM＋DN＝MN，试求∠MAN的大小．

 

 

Answer 1

（1）作图见试题解析；（2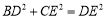），理由见试题解析；（3）45°．

【解析】

试题分析：（1）根据旋转的性质，作出图形即可；

（2）由旋转的性质容易得到BD=CF，∠ECF=90°，再由△ADE≌△AFE，可得DE=EF，从而得到BD，EC和DE之间的数量关系；

（3）将△ABN绕点A逆时针旋转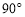，得到△ABE，从而得到E、B、M三点共线，在再由△AEM≌△ANM，即可得到∠MAN的度数．

试题解析：（1）如图，

（2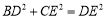），理由如下：

由旋转可知，AF=AD，CF=BD，∠DAF=90°，

∵∠DAE=45°，∴∠DAE=∠FAE=45°，

在△DAE和△FAE中，∵AD=AF，∠CAE=∠EAF，AE=AE，∴△DAE≌△FAE（SAS），∴EF=DE，

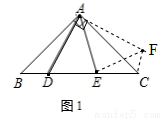
∵∠ECF=45°+45°=90°，∴，∴；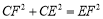

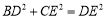（3） 将△ABN绕点A逆时针旋转，得到△ABE，如图：

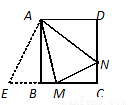
由旋转得：∠NAE=90°，AN=AE，∠ABE=∠D=90°，∴E、B、M三点共线，

∵BM+DN=MN，∴ME=MN，

又∵AM=AM，∴△AEM≌△ANM，∴∠MAE=∠MAN=45°．

考点：1．旋转的性质；2．全等三角形的判定与性质；3．正方形的性质．