
 如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )
如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )| A. | ①③ | B. | ①②④ | C. | ①②③④ | D. | ①③④ |
分析 ①易证∠CBE=∠DAE,即可求证:△ADE≌△BCE;
②根据①结论可得∠AEC=∠DEB,即可求得∠AED=∠BEG,即可解题;
③证明△AEF≌△BED即可;
④易证△FDC是等腰直角三角形,则CE=EF,S△AEF=S△ACE,由△AEF≌△BED,可知S△BDE=S△ACE,所以S△BDE=S△ACE.
解答 解:①∵AD为△ABC的高线,
∴∠ CBE+∠ABE+∠BAD=90°,
CBE+∠ABE+∠BAD=90°,
∵Rt△ABE是等腰直角三角形,
∴∠ABE=∠BAE=∠BAD+∠DAE=45°,AE=BE,
∴∠CBE+∠BAD=45°,
∴∠DAE=∠CBE,
在△DAE和△CBE中,
$\left\{\begin{array}{l}{AE=BE}\\{∠DAE=∠CBE}\\{AD=BC}\end{array}\right.$,
∴△ADE≌△BCE(SAS);
故①正确;
②∵△ADE≌△BCE,
∴∠EDA=∠ECB,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠ECB=90°,
∴∠DEC=90°,
∴CE⊥DE;
故②正确;
③∵∠BDE=∠ADB+∠ADE,∠AFE=∠ADC+∠ECD,
∴∠BDE=∠AFE,
∵∠BED+∠BEF=∠AEF+∠BEF=90°,
∴∠BED=∠AEF,
在△AEF和△BED中,
$\left\{\begin{array}{l}{∠BDE=∠AFE}\\{∠BED=∠AEF}\\{AE=BE}\end{array}\right.$,
∴△AEF≌△BED(AAS),
∴BD=AF;
故③正确;
④∵AD=BC,BD=AF,
∴CD=DF,
∵AD⊥BC,
∴△FDC是等腰直角三角形,
∵DE⊥CE,
∴EF=CE,
∴S△AEF=S△ACE,
∵△AEF≌△BED,
∴S△AEF=S△BED,
∴S△BDE=S△ACE.
故④正确;
故选C.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BFE≌△CDE是解题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
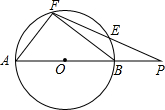 如图,点P在⊙O的直径AB的延长线上,PEF是⊙O的割线,且AF=FE,$\frac{PB}{PE}=\frac{5}{6}$,△ABF的面积为96.
如图,点P在⊙O的直径AB的延长线上,PEF是⊙O的割线,且AF=FE,$\frac{PB}{PE}=\frac{5}{6}$,△ABF的面积为96.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
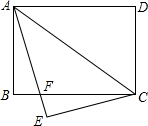 如图,矩形ABCD中,AB=6,BC=8,将△ACD沿对角线AC翻折得△ACE,AE交BC于点F,将△CEF绕点C逆时针旋转α角(0°<α<180°)得△CE′F′,点E、F的对应点分别为E、F的对应点分别为E′、F′.旋转过程中直线CF′、E′F′分别交直线AE于点M、N,当△F′NM是等腰三角形且MN=MF′时,则MN=$\frac{275}{56}$.
如图,矩形ABCD中,AB=6,BC=8,将△ACD沿对角线AC翻折得△ACE,AE交BC于点F,将△CEF绕点C逆时针旋转α角(0°<α<180°)得△CE′F′,点E、F的对应点分别为E、F的对应点分别为E′、F′.旋转过程中直线CF′、E′F′分别交直线AE于点M、N,当△F′NM是等腰三角形且MN=MF′时,则MN=$\frac{275}{56}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
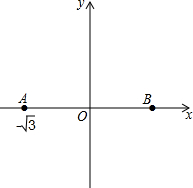 如图,在平面直角坐标系中,点A的坐标为(-$\sqrt{3}$,0),点A关于原点的对称点为B
如图,在平面直角坐标系中,点A的坐标为(-$\sqrt{3}$,0),点A关于原点的对称点为B查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b>a>c | B. | b>c>a | C. | a>b>c | D. | c>a>b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
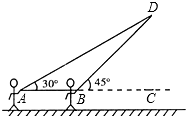 放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,最后结果精确到1米).
放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,最后结果精确到1米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com