
如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(
 ≈2.236,结果精确到0.1m)
≈2.236,结果精确到0.1m)


【考点】解直角三角形的应用-坡度坡角问题.
【分析】(1)根据坡度定义直接解答即可;
(2)作DS⊥BC,垂足为S,且与AB相交于H.证出∠GDH=∠SBH,根据
 =
=
 ,得到GH=1m,利用勾股定理求出DH的长,然后求出BH=5m,进而求出HS,然后得到DS.
,得到GH=1m,利用勾股定理求出DH的长,然后求出BH=5m,进而求出HS,然后得到DS.
【解答】解:(1)∵坡度为i=1:2,AC=4m,
∴BC=4×2=8m.
(2)作DS⊥BC,垂足为S,且与AB相交于H.
∵∠DGH=∠BSH,∠DHG=∠BHS,
∴∠GDH=∠SBH,
∴
 =
=
 ,
,
∵DG=EF=2m,
∴GH=1m,
∴DH=
 =
=
 m,BH=BF+FH=3.5+(2.5﹣1)=5m,
m,BH=BF+FH=3.5+(2.5﹣1)=5m,
设HS=xm,则BS=2xm,
∴x2+(2x)2=52,
∴x=
 m,
m,
∴DS=
 +
+
 =2
=2
 m≈4.5m.
m≈4.5m.


【点评】本题考查了解直角三角形的应用﹣﹣坡度坡角问题,熟悉坡度坡角的定义和勾股定理是解题的关键.


科目:初中数学 来源: 题型:
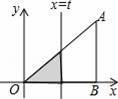
如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )

A.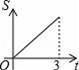
 B.
B.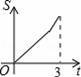
 C.
C.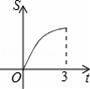
 D.
D.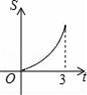

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为 .(用含n的代数式表示,n为正整数)
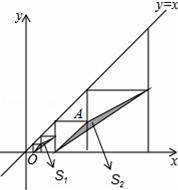

查看答案和解析>>
科目:初中数学 来源: 题型:
(1)数学课上,老师出了一道题,如图①,Rt△ABC中,∠C=90°,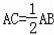
 ,求证:∠B=30°,请你完成证明过程.
,求证:∠B=30°,请你完成证明过程.
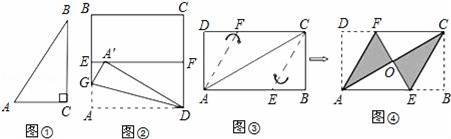
(2)如图②,四边形ABCD是一张边长为2的正方形纸片,E、F分别为AB、CD的中点,沿过点D的抓痕将纸片翻折,使点A落在EF上的点A′处,折痕交AE于点G,请运用(1)中的结论求∠ADG的度数和AG的长.
(3)若矩形纸片ABCD按如图③所示的方式折叠,B、D两点恰好重合于一点O(如图④),当AB=6,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
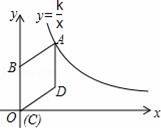
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=
 (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=
 (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com